题目内容
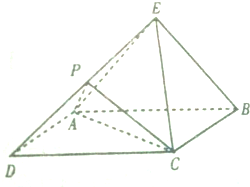 如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.
如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.(1)证明:P为ED中点;
(2)若AB=EC=2,AE=BE=
| 2 |
考点:平面与平面垂直的判定,直线与平面平行的性质
专题:空间位置关系与距离
分析:(1)连结BD,交AC于Q,连结PQ,则直线PQ与直线BE共面于BDE,BE∥平面PAC,PQ?平面PAC,得BE∥PQ,由此能证明P是DE的中点.
(2)取AB的中点O,连接EO,CO.由题意,可得△AEB是以AB为斜边的等腰直角三角形,得EO⊥AB,再由等边三角形△ACB的高线CO=
,得到平方关系:EC2=EO2+CO2,得EO⊥CO,所以EO⊥平面ABCD,从而得到平面EAB⊥平面ABCD.
(2)取AB的中点O,连接EO,CO.由题意,可得△AEB是以AB为斜边的等腰直角三角形,得EO⊥AB,再由等边三角形△ACB的高线CO=
| 3 |
解答:
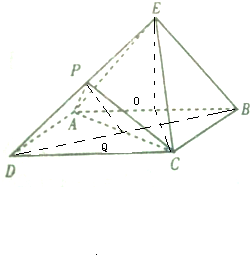 (1)证明:连结BD,交AC于Q,连结PQ,
(1)证明:连结BD,交AC于Q,连结PQ,
则直线PQ与直线BE共面于BDE,
∵BE∥平面PAC,PQ?平面PAC,
∴BE∥PQ,
∵ABCD为菱形,∴Q是BD中点,
∴P是DE的中点.
(2)取AB的中点O,连接EO,CO
∵△AEB中,AE=EB=
,
∴AE2+EB2=2=AB2,得△AEB为等腰直角三角形,
∴EO⊥AB,EO=1,
又∵△ABC中,AB=BC,∠ABC=60°
∴△ACB是等边三角形,得CO=
AB=
,
又∵EC=2,∴△ECO中,EC2=4=EO2+CO2,得EO⊥CO,
∵AB、CO是平面ABCD内的相交直线,∴EO⊥平面ABCD,
又∵EO?平面EAB,∴平面EAB⊥平面ABCD.
 (1)证明:连结BD,交AC于Q,连结PQ,
(1)证明:连结BD,交AC于Q,连结PQ,则直线PQ与直线BE共面于BDE,
∵BE∥平面PAC,PQ?平面PAC,
∴BE∥PQ,
∵ABCD为菱形,∴Q是BD中点,
∴P是DE的中点.
(2)取AB的中点O,连接EO,CO
∵△AEB中,AE=EB=
| 2 |
∴AE2+EB2=2=AB2,得△AEB为等腰直角三角形,
∴EO⊥AB,EO=1,
又∵△ABC中,AB=BC,∠ABC=60°
∴△ACB是等边三角形,得CO=
| ||
| 2 |
| 3 |
又∵EC=2,∴△ECO中,EC2=4=EO2+CO2,得EO⊥CO,
∵AB、CO是平面ABCD内的相交直线,∴EO⊥平面ABCD,
又∵EO?平面EAB,∴平面EAB⊥平面ABCD.
点评:本题给出特殊四棱锥,求证面面垂直并求二面角的余弦值,着重考查了空间线面垂直、面面垂直的判定与性质和利用空间向量的方法求面面所成角的知识,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
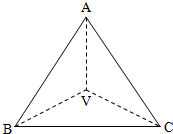 如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.
如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.
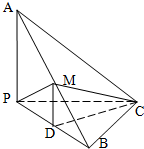 如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.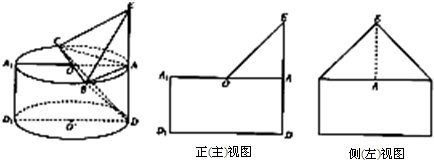
 如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点MN分别为A1B和B1C1的中点.
如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点MN分别为A1B和B1C1的中点.