题目内容
已知数列{an}的前n项和Sn=-an-(
)n-1+2(n为正整数).
(Ⅰ)令bn=2nan,求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)令cn=
an,Tn=c1+c2+…+cn试比较Tn与
的大小,并予以证明.
| 1 |
| 2 |
(Ⅰ)令bn=2nan,求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)令cn=
| n+1 |
| n |
| 5n |
| 2n+1 |
考点:数学归纳法,数列的求和,等差数列的性质
专题:综合题,点列、递归数列与数学归纳法
分析:(Ⅰ)由题意知S1=-a1-1+2=a1,an=Sn-Sn-1=-an+an-1+(
)n-1,所以2nan=2n-1an-1+1,bn=bn-1+1,再由b1=2a1=1,知数列bn是首项和公差均为1的等差数列.于是bn=1+(n-1)•1=n=2nan,所以an=
;
(Ⅱ)确定数列的通项,利用错位相减求和法,确定Tn与
的大小关系等价于比较2n与2n+1的大小.猜想当n=1,2时,2n<2n+1,当n≥3时,2n>2n+1.然后用数学归纳法证明.
| 1 |
| 2 |
| n |
| 2n |
(Ⅱ)确定数列的通项,利用错位相减求和法,确定Tn与
| 5n |
| 2n+1 |
解答:
解:(Ⅰ)在Sn=-an-(
)n-1+2中,令n=1,可得S1=-an-1+2=a1,即a1=
…1
当n≥2时,Sn-1=-an-1-(
)n-2+2,∴an=Sn-Sn-1=-an+an-1+(
)n-1,…2
∴2an=an-1+(
)n-1,即2nan=2n-1an-1+1.
∵bn=2nan,∴bn=bn-1+1,
即当n≥2时,bn-bn-1=1
又b1=2a1=1,∴数列{bn}是首项和公差均为1的等差数列…4
于是bn=1+(n-1)•1=n=2nan,
∴an=
…6
(II)由(I)得cn=
an=(n+1)(
)n,所以
Tn=2×
+3×(
)2+…+(n+1)•(
)n
∴
Tn=2×(
)2+3×(
)3…+n•(
)n+(n+1)(
)n+1
由①-②得
Tn=1+(
)2+(
)3…+(
)n-(n+1)(
)n+1
∴Tn=3-
…9
Tn-
=3-
-
=
…11
于是确定Tn与
的大小关系等价于比较2n与2n+1的大小
猜想当n=1,2时,2n<2n+1,当n≥3时,2n>2n+1.证明如下:
(1)当n=3时,由猜想显然成立.
(2)假设n=k时猜想成立.即2k>2k+1
则n=k+1时,2k+1=2•2k>2(2k+1)=4k+2=2(k+1)+1+(2k-1)>2(k+1)+1
所以当n=k+1时猜想也成立
综合(1)(2)可知,对一切n≥3的正整数,都有2n>2n+1.
| 1 |
| 2 |
| 1 |
| 2 |
当n≥2时,Sn-1=-an-1-(
| 1 |
| 2 |
| 1 |
| 2 |
∴2an=an-1+(
| 1 |
| 2 |
∵bn=2nan,∴bn=bn-1+1,
即当n≥2时,bn-bn-1=1
又b1=2a1=1,∴数列{bn}是首项和公差均为1的等差数列…4
于是bn=1+(n-1)•1=n=2nan,
∴an=
| n |
| 2n |
(II)由(I)得cn=
| n+1 |
| n |
| 1 |
| 2 |
Tn=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由①-②得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Tn=3-
| n+3 |
| 2n |
Tn-
| 5n |
| 2n+1 |
| n+3 |
| 2n |
| 5n |
| 2n+1 |
| (n+3)(2n-2n-1) |
| 2n(2n+1) |
于是确定Tn与
| 5n |
| 2n+1 |
猜想当n=1,2时,2n<2n+1,当n≥3时,2n>2n+1.证明如下:
(1)当n=3时,由猜想显然成立.
(2)假设n=k时猜想成立.即2k>2k+1
则n=k+1时,2k+1=2•2k>2(2k+1)=4k+2=2(k+1)+1+(2k-1)>2(k+1)+1
所以当n=k+1时猜想也成立
综合(1)(2)可知,对一切n≥3的正整数,都有2n>2n+1.
点评:本题考查数列和不等式的综合运用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意数学归纳法的灵活运用.

练习册系列答案
相关题目
若(a+2i)i=b+i,其中a,b∈R,i是虚数单位,则a-b=( )
| A、-3 | B、-2 | C、2 | D、3 |
线性回归方程表示的直线
=bx+a必经过( )
 |
| y |
| A、(0,0) | ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
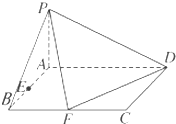 已知四棱锥P-ABCD底面ABCD是矩形PA⊥平面ABCD,AD=2,AB=1,E、F分别是线段AB,BC的中点,
已知四棱锥P-ABCD底面ABCD是矩形PA⊥平面ABCD,AD=2,AB=1,E、F分别是线段AB,BC的中点,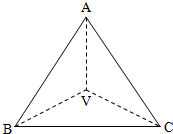 如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.
如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.