题目内容
设函数f(x)=lg(-x2+5x-6)的定义域为A,函数g(x)=
,x∈(0,m)的值域为B.
(Ⅰ)当m=2时,求A∩B;
(Ⅱ)若“x∈A”是“x∈B”的必要不充分条件,求实数m的取值范围.
| 5 |
| x+2 |
(Ⅰ)当m=2时,求A∩B;
(Ⅱ)若“x∈A”是“x∈B”的必要不充分条件,求实数m的取值范围.
考点:必要条件、充分条件与充要条件的判断,交集及其运算
专题:集合
分析:(Ⅰ)当m=2时,求出集合A,B,即可求A∩B;
(Ⅱ)若“x∈A”是“x∈B”的必要不充分条件,建立集合关系即可求实数m的取值范围
(Ⅱ)若“x∈A”是“x∈B”的必要不充分条件,建立集合关系即可求实数m的取值范围
解答:
解:(Ⅰ)由-x2+5x-6>0,即x2-5x+6<0,解得2<x<3,即A=(2,3),
当m=2时,g(x)=
,x∈(0,2)上为减函数,
∴
<g(x)<
,即B=(
,
),
则A∩B=(2,
);
(Ⅱ)∵g(x)=
,x∈(0,m)上为减函数,
∴
<g(x)<
,即B=(
,
)
若“x∈A”是“x∈B”的必要不充分条件,
则B?A,
即
,则
,
即0<m≤
,
故实数m的取值范围是(0,
].
当m=2时,g(x)=
| 5 |
| x+2 |
∴
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
则A∩B=(2,
| 5 |
| 2 |
(Ⅱ)∵g(x)=
| 5 |
| x+2 |
∴
| 5 |
| 2+m |
| 5 |
| 2 |
| 5 |
| 2+m |
| 5 |
| 2 |
若“x∈A”是“x∈B”的必要不充分条件,
则B?A,
即
|
|
即0<m≤
| 1 |
| 2 |
故实数m的取值范围是(0,
| 1 |
| 2 |
点评:本题主要考查函数的基本运算以及充分条件和必要条件的应用,根据条件求出函数的定义域和值域是解决本题的关键.

练习册系列答案
相关题目
已知直线mx+2y-5=0与直线2x+y-1=0垂直,则m的值为( )
| A、-1 | B、0 | C、PAD | D、4 |
已知M={-3,-2,0,1,2},N={-2,-1,1,2},则M∩N=( )
| A、{-2,1,2 } |
| B、{-3,-2,-1,0,1,2} |
| C、M |
| D、N |
函数y=
+(x-1)0的定义域为( )
| ||
| x-2 |
| A、{x|x≥1} |
| B、{x|x≥1 且x≠2} |
| C、{x|x>1} |
| D、{x|x>1 且x≠2} |
若直线x-2y+5=0与直线2x+my-6=0互相垂直,则实数m等于( )
| A、1 | ||
| B、2 | ||
| C、4 | ||
D、
|
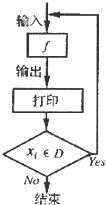 对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下: