题目内容
数列{an}的前n项和Sn=n2，则它的通项公式是 ．
考点：数列递推式
专题：等差数列与等比数列
分析：根据数列通项公式和前n项和之间的关系即可得到结论．
解答：
解：∵数列{an}的前n项和Sn=n2，
∴当n≥2时，an=Sn-Sn-1=n2-（n-1）2=2n-1，
当n=1，a1=S1=1满足an=2n-1，
即数列{an}的通项公式为an=2n-1，
故答案为：an=2n-1
∴当n≥2时，an=Sn-Sn-1=n2-（n-1）2=2n-1，
当n=1，a1=S1=1满足an=2n-1，
即数列{an}的通项公式为an=2n-1，
故答案为：an=2n-1
点评：本题主要考查数列通项公式的求解，根据数列通项公式和前n项和之间的关系是解决本题的关键．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
从6本不同的数学书和5本不同的英语书中取3本，要求数学书和英语书都要有取到，则不同的取法种数有（ ）种．
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
（x+1）5展开式的二项式系数的和是（ ）
| A、6 | B、128 | C、32 | D、64 |
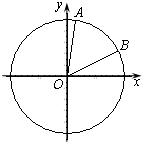如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α、β，它们的终边分别交单位圆于A、B两点．已知A、B两点的横坐标分别是
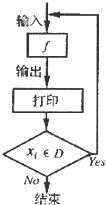对任意函数f（x），x∈D，可按图示构造一个数列发生器，其工作原理如下：