题目内容
已知定义在R上的偶函数y=f(x),且x≥0时,f(x)=2x-1
(1)当x<0时,求f(x)的解析式;
(2)当x∈[-1,m](m>-1)时,求函数f(x)的值域.
(1)当x<0时,求f(x)的解析式;
(2)当x∈[-1,m](m>-1)时,求函数f(x)的值域.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)求x<0时的f(x)解析式,所以设x<0,-x>0,从而可求出f(x)=f(-x)=2-x-1;
(2)根据f(x)的单调性,分m≤0,0<m≤1,m>1这几种情况讨论m的取值,然后根据f(x)的单调性及最值情况即可求得f(x)在[-1,m]上的值域.
(2)根据f(x)的单调性,分m≤0,0<m≤1,m>1这几种情况讨论m的取值,然后根据f(x)的单调性及最值情况即可求得f(x)在[-1,m]上的值域.
解答:
解:(1)设x<0,-x>0;
∴f(x)=f(-x)=2-x-1;
即x<0时,f(x)=2-x-1;
(2)容易判断x≥0时,f(x)=2x-1是增函数;
x<0时,f(x)=2-x-1是减函数;
∴①若m≤0,f(x)的值域为[f(-1),f(m)]=[1,2-m-1];
②若0<m≤1,则2m-1≤1,∴此时f(x)的值域为[f(0),f(-1)]=[
,1];
③若m>1,则2m-1>1,∴此时f(x)的值域为[f(0),f(m)]=[
,2m-1].
∴f(x)=f(-x)=2-x-1;
即x<0时,f(x)=2-x-1;
(2)容易判断x≥0时,f(x)=2x-1是增函数;
x<0时,f(x)=2-x-1是减函数;
∴①若m≤0,f(x)的值域为[f(-1),f(m)]=[1,2-m-1];
②若0<m≤1,则2m-1≤1,∴此时f(x)的值域为[f(0),f(-1)]=[
| 1 |
| 2 |
③若m>1,则2m-1>1,∴此时f(x)的值域为[f(0),f(m)]=[
| 1 |
| 2 |
点评:考查求偶函数在对称区间上的解析式的方法与过程,根据分段函数的单调性及单调区间,讨论参数m的取值范围,从而求函数的值域.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
执行下面的程序框图,则输出结果是( )


A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
已知函数y=f(x)是偶函数,且y=f(x)在[0,2]上是减函数,则( )
| A、f(2)<f(-1)<f(0) |
| B、f(-1)<f(0)<f(2) |
| C、f(-1)<f(2)<f(0) |
| D、f(0)<f(-1)<f(2) |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A、y=cosx | ||
| B、y=ln|x| | ||
C、y=
| ||
| D、y=tan2x |
设函数f(x)=
是R上的单调递减函数,则实数a的取值范围为( )
|
A、(-∞,
| ||
| B、(-∞,2) | ||
| C、(0,2) | ||
D、[
|
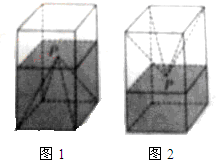 如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2),有下列三个命题:
如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2),有下列三个命题: