题目内容
已知双曲线
-
=1(a>0,b>0)的焦点分别为F1、F2,以F1F2为直径的圆交双曲线于点A,若∠F1F2A=
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、1+
| ||
B、4+2
| ||
C、4-
| ||
D、2+
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据F1F2为圆的直径,推断出∠F1AF2为直角,进而结合∠F1F2A=
,可得|AF1|和|AF2|,根据双曲线的定义求得a,则双曲线的离心率可得.
| π |
| 6 |
解答:
解:∵F1F2为圆的直径,
∴△AF1F2为直角三角形,
又∵∠F1F2A=
,
∴|AF1|=c,|AF2|=
c,
根据双曲线的定义可知a=
,
∴e=
=
=
=1+
.
故选:A.
∴△AF1F2为直角三角形,
又∵∠F1F2A=
| π |
| 6 |
∴|AF1|=c,|AF2|=
| 3 |
根据双曲线的定义可知a=
(
| ||
| 2 |
∴e=
| c |
| a |
| c | ||||
|
| 2 | ||
|
| 3 |
故选:A.
点评:本题主要考查了双曲线的简单性质.考查了学生数形结合思想的运用和基本的运算能力.

练习册系列答案
相关题目
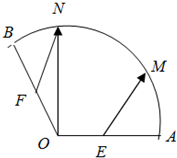 如图,扇形OAB的半径OA=2,∠AOB=120°,点E是OA的中点,点F是OB的中点,点M,N分别是
如图,扇形OAB的半径OA=2,∠AOB=120°,点E是OA的中点,点F是OB的中点,点M,N分别是