题目内容
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
(1)求函数f(x)的解析式,并写出它的单调减区间;
(2)当x∈[-6,-
| 2 |
| 3 |
(3)记S=f(0)+f(1)+…+f(2014),求S的值.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:综合题,三角函数的图像与性质
分析:(1)由图知A=2,
T=4,易求ω=
;又1×
+φ=2kπ+
(k∈Z),|φ|<
,可求得φ,从而可得函数f(x)的解析式及其单调减区间;
(2)当x∈[-6,-
]时,x+2∈[-4,
],
(x+2)+
∈[-
,
],利用正弦函数的单调性可求函数y=f(x+2)的值域;
(3)利用f(x)=2sin(
x+
)的周期T=8,即可求得S=f(0)+f(1)+…+f(2014)的值.
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
(2)当x∈[-6,-
| 2 |
| 3 |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 7π |
| 12 |
(3)利用f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
解答:
解:(1)由图知A=2,
T=3-(-1)=4,T=8,
∴ω=
=
;
又1×
+φ=2kπ+
(k∈Z),
∴φ=2kπ+
(k∈Z),又|φ|<
,
∴φ=
,
∴f(x)=2sin(
x+
);
由2kπ+
≤
x+
≤2kπ+
(k∈Z),得:8k+1≤x≤8k+5(k∈Z),
∴f(x)=2sin(
x+
)的单调递减区间为[8k+1,8k+5](k∈Z);
(2)当x∈[-6,-
]时,x+2∈[-4,
],
(x+2)+
∈[-
,
],
∴-2≤f(x)=2sin(
x+
)≤2,
即y=f(x+2)的值域为[-2,2].
(3)∵f(0)=
,f(1)=2,f(2)=
,f(3)=0,f(4)=-
,f(5)=-2,f(6)=-
,f(7)=0,
∴f(0)+f(1)+…+f(7)=0,
∵f(x)=2sin(
x+
)的周期T=8,2015=251×8+7=252×8-1,
∴S=f(0)+f(1)+…+f(2014)=252×0-f(7)=252
-0=0.
| 1 |
| 2 |
∴ω=
| 2π |
| T |
| π |
| 4 |
又1×
| π |
| 4 |
| π |
| 2 |
∴φ=2kπ+
| π |
| 4 |
| π |
| 2 |
∴φ=
| π |
| 4 |
∴f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
由2kπ+
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 2 |
∴f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
(2)当x∈[-6,-
| 2 |
| 3 |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 7π |
| 12 |
∴-2≤f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
即y=f(x+2)的值域为[-2,2].
(3)∵f(0)=
| 2 |
| 2 |
| 2 |
| 2 |
∴f(0)+f(1)+…+f(7)=0,
∵f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
∴S=f(0)+f(1)+…+f(2014)=252×0-f(7)=252
| 2 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的单调性,考查图象变换与数列求和,属于难题.

练习册系列答案
相关题目
sin
+cos
-tan(-
)=( )
| 25π |
| 6 |
| 25π |
| 3 |
| 25π |
| 4 |
| A、0 | B、1 | C、2 | D、-2 |
圆C:x2+y2-2x-4y+4=0的圆心到直线l:3x+4y+4=0的距离为( )
A、3
| ||
| B、2 | ||
| C、3 | ||
D、
|
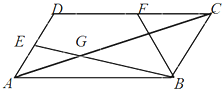 如图所示,在平行四边形ABCD中,∠BAD=
如图所示,在平行四边形ABCD中,∠BAD=