题目内容
已知函数f(x)=
cos(x-
),x∈R.
(1)求f(
)及f(-
)的值;
(2)若cosθ=
,θ∈(
,2π),求f(θ-
)和f(2θ+
)的值.
| 2 |
| π |
| 12 |
(1)求f(
| π |
| 3 |
| π |
| 6 |
(2)若cosθ=
| 3 |
| 5 |
| 3π |
| 2 |
| π |
| 6 |
| π |
| 3 |
考点:三角函数的恒等变换及化简求值
专题:计算题,三角函数的求值
分析:(1)将x=
及-
代入,结合特殊角的三角函数值,可得答案;
(2)根据cosθ=
,θ∈(
,2π),求出sinθ,代入两角差的余弦公式,可得答案.
| π |
| 3 |
| π |
| 6 |
(2)根据cosθ=
| 3 |
| 5 |
| 3π |
| 2 |
解答:
解:(1)f(
)=
cos(
-
)=
cos
=
×
=1,
f(-
)=
cos(-
-
)=
cos(-
)=
×
=1,
(2)(2)∵cosθ=
,θ∈(
,2π),
∴sinθ=-
=-
,
∴f(θ-
)=
cos(θ-
)=
(cosθcos
+sinθsin
)=-
.
f(2θ+
)=
cos(2θ+
)=cos2θ-sin2θ=2cos2θ-1+2sinθcosθ=-
.
| π |
| 3 |
| 2 |
| π |
| 3 |
| π |
| 12 |
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
f(-
| π |
| 6 |
| 2 |
| π |
| 6 |
| π |
| 12 |
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
(2)(2)∵cosθ=
| 3 |
| 5 |
| 3π |
| 2 |
∴sinθ=-
| 1-cos2θ |
| 4 |
| 5 |
∴f(θ-
| π |
| 6 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 5 |
f(2θ+
| π |
| 3 |
| 2 |
| π |
| 4 |
| 31 |
| 25 |
点评:本题考查的知识点是两角和与差的余弦公式,特殊角的三角函数值,难度不大,属于基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
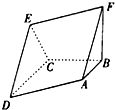 如图空间几何体ABCDEF中,四边形ADEF为平行四边形,FB⊥平面ABCD,AB∥CD,AB⊥BC,AB=BC=
如图空间几何体ABCDEF中,四边形ADEF为平行四边形,FB⊥平面ABCD,AB∥CD,AB⊥BC,AB=BC=