题目内容

某同学为了研究函数f（x）=
1+x2
+
1+(1-x)2
（0≤x≤1）的性质，构造了如图所示的两个边长为1的正方形ABCD和BEFC，点P是边BC上的一个动点，设CP=x，则f（x）=PF+AP．那么可推知方程f（x）=
6
解的个数是（　　）
A、0B、1C、2D、4
考点：根的存在性及根的个数判断
专题：计算题,函数的性质及应用
分析：由f（x）=PF+AP知，当点P在点C或B时，f（x）有最大值1+
2
；从而比较其与
6
的大小关系即可．
解答： 解：由f（x）=PF+AP知，
当点P在点C或B时，f（x）有最大值1+
2
；
而1+
2
＜
6
；
故没有x能使方程f（x）=
6
成立，
故方程f（x）=
6
无解．
故选A．
点评：本题考查了函数的几何意义的应用，属于基础题．
练习册系列答案
相关题目
通常候鸟每年秋天从北方飞往南方过冬，若某种候鸟的飞行速度y（m/s）可以表示为函数y=5log2
x
10
，其中x为这种候鸟在飞行过程中耗氧量的单位数．
（1）当这种候鸟的耗氧量是80个单位时，它的飞行速度是多少？
（2）当这种候鸟静止时，它的耗氧量是多少个单位？
已知f（x）是定义在[-3，3]上的偶函数，当x∈[0，3）时，f（x）=|x2-2x+
1
2
|，若函数y=f（x）-a在区间[-3，3]上有8个零点（互不相同），则实数a的取值范围是
 
．
圆（x-1）2+y2=1和圆x2+y2+2x+4y-4=0的位置关系为（　　）
A、相交B、相切
C、相离D、以上都有可能
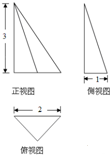某三棱锥的三视图如图所示，其正视图和侧视图都是直角三角形，则该三棱锥的体积等于（　　）
A、
1
3
B、
2
3
C、1
D、3
若点P是抛物线y2=4x上一点，A（5，3），F为抛物线的焦点，则|PA|+|PF|的最小值为
 
．
设双曲线的两个焦点分别为F1，F2，若双曲线上存在点P满足|PF1|：|F1F2|：|PF2|=6：5：3，则双曲线的离心率等于
 
．
观察式子1+
1
22
＜
3
2
，1+
1
22
+
1
32
＜
5
3
，1+
1
22
+
1
32
+
1
42
＜
7
4
…则可归纳出关于正整数n（n∈N*，n≥2）的式子为
 
．
已知向量
a
=（1，2），
b
=（1，0），
c
=（4，-3）．若λ为实数，（
a
+λ
b
）⊥
c
，则λ=（　　）
A、
1
4
B、
1
2
C、1
D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网