题目内容
观察式子1+
＜
，1+
+
＜
，1+
+
+
＜
…则可归纳出关于正整数n（n∈N*，n≥2）的式子为 ．
| 1 |
| 22 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
考点：归纳推理
专题：计算题,推理和证明
分析：根据规律，左边是正整数n的平方的倒数和，右边是分子是正奇数，分母是正整数n，可以猜想结论．
解答：
解：根据规律，左边是正整数n的平方的倒数和，右边是分子是正奇数，分母是正整数n，
可以猜想的结论为：当n∈N且n≥2时，恒有1+
+…+
＜
．
故答案为：1+
+…+
＜
可以猜想的结论为：当n∈N且n≥2时，恒有1+
| 1 |
| 22 |
| 1 |
| n2 |
| 2n-1 |
| n |
故答案为：1+
| 1 |
| 22 |
| 1 |
| n2 |
| 2n-1 |
| n |
点评：本题考查的知识点是归纳推理其中分析已知中的式子，分析出两个式子之间的数据变化规律是解答的关键．
练习册系列答案
相关题目
某同学为了研究函数f（x）=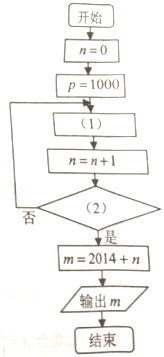
某电机厂2014年年底有资金1000万元，由于引进了先进生产设备，资金年平均增长率可达到50%，现在要设计一个程序，计算该电机厂的资金首次超过8000万元时，是哪一年的年底．