题目内容

2．如图，已知直线l1，l2，l3的斜率分别为k1，k2，k3，则（　　）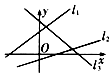
A．k1＜k2＜k3B．k3＜k2＜k1C．k1＜k3＜k2D．k2＜k1＜k3

分析 由于直线l1，l2的倾斜角都是锐角，且直线l1的倾斜角大于直线l2的倾斜角，可得k1＞k2＞0．由于直线l3的倾斜角为钝角，k3 ＜0，由此可得结论．

解答 解：由于直线l1，l2的倾斜角都是锐角，且直线l1的倾斜角大于直线l2的倾斜角，
故直线l1的斜率大于直线l2的斜率，即 k1＞k2＞0．
由于直线l3的倾斜角为钝角，故l3的斜率小于零，即k3 ＜0，
所以k3＜k2＜k1
故选：B．

点评 本题主要考查直线的倾斜角和斜率的关系，属于基础题．

练习册系列答案
相关题目
12．已知函数f（x）=ex-ax（a为常数），f′（x）是f（x）的导函数．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）当x＞0时，求证：f（lna+x）＞f（lna-x）；
（Ⅲ）已知f（x）有两个零点x1，x2（x1＜x2），求证：${f^/}（{\frac{{{x_1}+{x_2}}}{2}}）＜0$．
13．若直线l：y=kx+1与圆C：x2+y2-2x-3=0交于A，B，则|AB|的最小值为$2\sqrt{2}$ ．
10．函数f（x）=$\sqrt{3}$cos（x+2φ）是R上的奇函数，则φ可能是（　　）
A．0B．$\frac{π}{4}$C．$\frac{π}{2}$D．π
17．已知tanα=-$\frac{1}{2}$，求$\frac{1+2sin（π-α）cos（-2π-α）}{si{n}^{2}α-si{n}^{2}（\frac{5π}{2}-α）}$+$\frac{1}{3}$的值．
7．如图，已知AB⊥平面BCD，BC⊥CD．求证：
（1）平面ABC⊥平面ACD．
（2）写出图中所有的面面垂直．
14．设f（x）=ex（sinx-cosx），其中 0≤x≤2011π，则 f（x）的极大值点个数是（　　）
A．25B．1005C．26D．28
11．设P为函数f（x）=sinπx的图象上的一个最高点，Q为函数g（x）=cosπx的图象上的一个最低点．
（1）求|PQ|的最小值；
（2）求f（x）的图象与g（x）的图象的交点中，相邻的三个交点构成的三角形的面积；
（3）求函数f（x）的图象关于直线x=$\frac{1}{4}$对称的函数h（x）图象的解析式，并求出$x∈[-\frac{2}{3}，\frac{1}{3}]$的值域．
12．若复数Z=（x2-1）+（x2-3x+2）i，试求x的取值范围．
（1）Z是实数；
（2）Z是纯虚数；
（3）Z对应的点在复平面的第二象限．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网