题目内容
10.函数f(x)=$\sqrt{3}$cos(x+2φ)是R上的奇函数,则φ可能是( )| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
分析 根据函数是奇函数和余弦函数的性质可得答案.
解答 解:函数f(x)=$\sqrt{3}$cos(x+2φ)是R上的奇函数,∴f(0)=0,
即2φ=k$π+\frac{π}{2}$,(k∈Z)
当k=0时,φ=$\frac{π}{4}$.
故选B.
点评 本题考查了函数是奇函数和余弦函数的性质的运用,比较基础,

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
18.已知回归直线的斜率为-1,样本点中心为(1,2),则回归直线方程为( )
| A. | $\widehat{y}$=x+3 | B. | $\widehat{y}$=-x+3 | C. | $\widehat{y}$=-x-3 | D. | $\widehat{y}$=-2x+4 |
2.如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
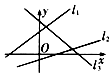

| A. | k1<k2<k3 | B. | k3<k2<k1 | C. | k1<k3<k2 | D. | k2<k1<k3 |