题目内容
7. 如图,已知AB⊥平面BCD,BC⊥CD.求证:
如图,已知AB⊥平面BCD,BC⊥CD.求证:(1)平面ABC⊥平面ACD.
(2)写出图中所有的面面垂直.
分析 (1)由AB⊥平面BCD,CD?平面BCD,可得AB⊥CD,根据CD⊥BC且AB∩BC=B,可得CD⊥平面ABC,由此可证结论.
(2)利用已知条件与(1)的结果,写出所有的面面垂直.
解答 (1) 证明:∵AB⊥平面BCD,CD?平面BCD,
证明:∵AB⊥平面BCD,CD?平面BCD,
∴AB⊥CD.
∵CD⊥BC且AB∩BC=B,
∴CD⊥平面ABC.
∵CD?平面ACD,
∴平面ACD⊥平面ABC.
(2)平面ABC⊥平面BCD,平面ABD⊥平面BCD,
平面ACD⊥平面ABC,平面BCD⊥平面ABC
点评 本题考查线面垂直、面面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知回归直线的斜率为-1,样本点中心为(1,2),则回归直线方程为( )
| A. | $\widehat{y}$=x+3 | B. | $\widehat{y}$=-x+3 | C. | $\widehat{y}$=-x-3 | D. | $\widehat{y}$=-2x+4 |
2.如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
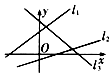

| A. | k1<k2<k3 | B. | k3<k2<k1 | C. | k1<k3<k2 | D. | k2<k1<k3 |
16.若圆C经过坐标原点和点(4,0),且与直线y=1相切,则圆C的方程是( )
| A. | ${(x-2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$ | B. | ${(x-2)^2}+{(y-\frac{3}{2})^2}=\frac{25}{4}$ | ||
| C. | ${(x+2)^2}+{(y-\frac{3}{2})^2}=\frac{25}{4}$ | D. | ${(x+2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$ |