题目内容
11.已知数列{an}的首项为-1,an+1=2an+2,则数列{an}的通项公式为an=( )| A. | 2n-1-2 | B. | 2n-2 | C. | 2n-1-2n | D. | -2n-1 |
分析 由题意可知an+1+2=2(an+2),根据等比数列的通项公式,即可求得数列{an}的通项公式an=2n-1-2.
解答 解:由an+1=2an+2,则an+1+2=2(an+2),
a1+2=1,
∴数列{an}是以1为首项,以2为公比的等比数列,
则an+2=1×2n-1,
∴an=2n-1-2,
∴数列{an}的通项公式an=2n-1-2,
故选:A.
点评 本题考查数列的递推式的应用,考查等比数列的前n项和公式,考查计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列描述不能看作算法的是( )
| A. | 做米饭需要刷锅,淘米,添水,加热这些步骤 | |
| B. | 洗衣机的使用说明书 | |
| C. | 利用公式S=πr2计算半径为4的圆的面积,就是计算π×42 | |
| D. | 解方程2x2+x-1=0 |
19.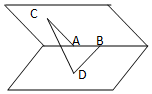 如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )
如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )
 如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )
如图在一个60°的二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 1 |
6.下列各函数中,最小值为4的是( )
| A. | $y=x+\frac{4}{x}$ | B. | $y=sinx+\frac{4}{sinx}(0<x<π)$ | ||
| C. | y=4log3x+logx3 | D. | y=4ex+e-x |
16.设实数x,y满足约束条件$\left\{\begin{array}{l}{3x-2y+4≥0}\\{x+ay-4≤0}\\{x-y-2≤0}\end{array}\right.$,已知z=2x+y的最大值是7,最小值是-26,则实数a的值为( )
| A. | 6 | B. | -6 | C. | -1 | D. | 1 |
3.若抛物线y2=2px的焦点与双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{1}$=1的右焦点重合,则p的值为( )
| A. | 2$\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
9.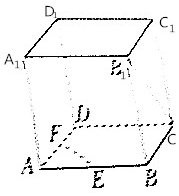 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |