题目内容
已知函数f(x)=ax2-2x+c(a,c∈R)满足条件:①f(1)=0;②对一切x∈R,都有f(x)≥0.
(1)求f(x)的解析式;
(2)是否存在实数m,使函数g(x)=f(x)-4mx在区间[m,m+2]上有最小值-20?若存在,请求出实数m的值;若不存在,请说明理由.
(1)求f(x)的解析式;
(2)是否存在实数m,使函数g(x)=f(x)-4mx在区间[m,m+2]上有最小值-20?若存在,请求出实数m的值;若不存在,请说明理由.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:函数的性质及应用
分析:(1)分a=0和a函数是二次函数,再利用二次函数的性质解决对一切x∈R,都有f(x)≥0;根据f(1)=0得,
(2)g(x)=f(x)-4mx=x2-(4m+2)x+1,该函数图象开口向上,且对称轴为x=2m+1,假设存在实数m使函数g(x)=f(x)-4mx=x2-(4m+2)x+1 在区间[m,m+2]上有最小值-20.根据函数的对称轴与区间的关系进行分类讨论,从而可求m的值.
(2)g(x)=f(x)-4mx=x2-(4m+2)x+1,该函数图象开口向上,且对称轴为x=2m+1,假设存在实数m使函数g(x)=f(x)-4mx=x2-(4m+2)x+1 在区间[m,m+2]上有最小值-20.根据函数的对称轴与区间的关系进行分类讨论,从而可求m的值.
解答:
解:(1)当a=0时,f(x)=-2x+c.
由f(1)=0得-2+c=0,即c=2,
∴f(x)=-2x+2,
显然x>1时,f(x)<0,这与条件②相矛盾,
∴a≠0,因而函数f(x)=ax2-2x+c是二次函数,
由于对一切x∈R,都有f(x)≥0,由二次函数的性质可得
,即
,由此可知 a>0,c>0,
∴ac≤(
)2,
由f(1)=0,得a+c=2,代入上式得ac≤1.
但前面已推得ac≥1,
∴ac=1,
综上解得a=c=1,
∴f(x)的解析式为f(x)=x2-2x+1,
(2)由题意g(x)=f(x)-4mx=x2-2x+1-4mx=x2-(4m+2)x+1,
该函数图象开口向上,且对称轴为x=2m+1,
假设存在实数m使函数g(x)=f(x)-4mx=x2-(4m+2)x+1在区间[m,m+2]上有最小值-5.
①当m<-1时,2m+1<m,函数g(x)在区间[m,m+2]上是递增的,
∴g(m)=-20,
即m2-(4m+2)m+1=-20,化简得3m2+2m-21=0,
解得m=-3或m=
(与m<-1矛盾,舍去),
②当-1≤m<1时,m≤2m+1<m+1,函数g(x)在区间[m,2m+1]上是递减的,而在区间[2m+1,m+2]上递增,
∴g(2m+1)=-20,
即(2m+1)2-(4m+2)(2m+1)+1=-20,
解得m=
或m=
,与-1≤m<1矛盾,都舍去,
③当m≥1时,2m+1≥m+2,函数g(x)在区间[m,m+2]上是递减的,
∴g(m+2)=-20,
即(m+2)2-(4m+2)(m+2)+1=-20,
解得m=-1-2
(与m≥1矛盾,舍去)或m=-1+2
,
综上可得,当m=-3或m=-1+2
时,函数g(x)=f(x)-4mx在区间[m,m+2]上有最小值-20.
由f(1)=0得-2+c=0,即c=2,
∴f(x)=-2x+2,
显然x>1时,f(x)<0,这与条件②相矛盾,
∴a≠0,因而函数f(x)=ax2-2x+c是二次函数,
由于对一切x∈R,都有f(x)≥0,由二次函数的性质可得
|
|
∴ac≤(
| a+c |
| 2 |
由f(1)=0,得a+c=2,代入上式得ac≤1.
但前面已推得ac≥1,
∴ac=1,
综上解得a=c=1,
∴f(x)的解析式为f(x)=x2-2x+1,
(2)由题意g(x)=f(x)-4mx=x2-2x+1-4mx=x2-(4m+2)x+1,
该函数图象开口向上,且对称轴为x=2m+1,
假设存在实数m使函数g(x)=f(x)-4mx=x2-(4m+2)x+1在区间[m,m+2]上有最小值-5.
①当m<-1时,2m+1<m,函数g(x)在区间[m,m+2]上是递增的,
∴g(m)=-20,
即m2-(4m+2)m+1=-20,化简得3m2+2m-21=0,
解得m=-3或m=
| 7 |
| 3 |
②当-1≤m<1时,m≤2m+1<m+1,函数g(x)在区间[m,2m+1]上是递减的,而在区间[2m+1,m+2]上递增,
∴g(2m+1)=-20,
即(2m+1)2-(4m+2)(2m+1)+1=-20,
解得m=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
③当m≥1时,2m+1≥m+2,函数g(x)在区间[m,m+2]上是递减的,
∴g(m+2)=-20,
即(m+2)2-(4m+2)(m+2)+1=-20,
解得m=-1-2
| 2 |
| 2 |
综上可得,当m=-3或m=-1+2
| 2 |
点评:本小题主要考查函数、方程、不等式等基本知识,考查综合运用数学知识分析和解决问题的能力,本题考查的重点是函数的解析式的求解与函数最值的研究,解题的关键是合理运用函数的性质,正确分类,同时考查学生分析解决问题的能力,有一定的综合性.

练习册系列答案
相关题目
已知数列{an}的通项为an=n2-2λn,则“λ<0”是“?n∈N*,an+1>an”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
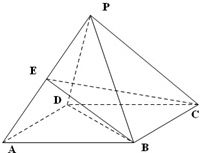 已知四棱锥P-ABCD的底面是正方形,PB=PD,E为PA的中点.
已知四棱锥P-ABCD的底面是正方形,PB=PD,E为PA的中点.