题目内容
16．已知直线x-ay=4在y轴上的截距是2，则a等于（ ）| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -2 | D． | 2 |
分析 直接把点（0，2）代入直线方程，求出a即可．
解答 解：已知直线x-ay=4在y轴上的截距是2，
即直线过（0，2），代入得：-2a=4，
则a=-2，
故选：C．
点评 本题考查了一次函数图象上点的坐标的特点，是一道基础题．
练习册系列答案
寒假学与练系列答案
相关题目
7．对于函数f（x），若存在x0∈Z，满足|f（x0）|≤$\frac{1}{4}$，则称x0为函数f（x）的一个“近零点”．已知函数f（x）=ax2+bx+c（a＞0）有四个不同的“近零点”，则a的最大值为（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
1．若函数f（x）=$\frac{x-4}{m{x}^{2}+4mx+3}$的定义域为R，则实数m的取值范围是（ ）
| A． | （0，$\frac{3}{4}$） | B． | （0，$\frac{3}{4}$] | C． | [0，$\frac{3}{4}$] | D． | [0，$\frac{3}{4}$） |
5．
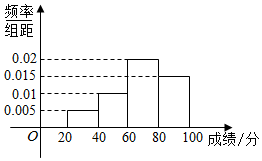某班全体学生参加一次测试，将所得分数依次分组：[20，40），[40，60），[60，80），[80，100），绘制出如图所示的成绩频率分布直方图，若低于60分的人数是18，则该班的学生人数是（ ）
某班全体学生参加一次测试，将所得分数依次分组：[20，40），[40，60），[60，80），[80，100），绘制出如图所示的成绩频率分布直方图，若低于60分的人数是18，则该班的学生人数是（ ）| A． | 50 | B． | 54 | C． | 60 | D． | 64 |
6．已知圆锥的母线长为20cm，则当其体积最大时，其侧面积为（ ）
| A． | $\frac{800\sqrt{6}π}{3}$cm2 | B． | $\frac{400\sqrt{6}π}{3}$cm2 | C． | $\frac{100\sqrt{6}π}{3}$cm2 | D． | $\frac{200\sqrt{6}π}{3}$cm2 |