题目内容
19.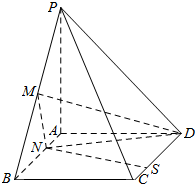 已知四棱锥P-ABCD中,面ABCD为矩形,PA⊥面ABCD,$PA=AD=\frac{1}{2}AB$,M为PB的中点,N、S分别为AB、CD上的点,且$AN=CS=\frac{1}{4}AB$.
已知四棱锥P-ABCD中,面ABCD为矩形,PA⊥面ABCD,$PA=AD=\frac{1}{2}AB$,M为PB的中点,N、S分别为AB、CD上的点,且$AN=CS=\frac{1}{4}AB$.(1)证明:DM⊥SN;
(2)求SN与平面DMN所成角的余弦值.
分析 (1)取AB中点E,连接EM、ED,推导出EM⊥SN,ES⊥ED,由此能证明SN⊥DM.
解:设PA=1,以A为原点,射线AB,AD,AP分别为x,y,z轴正方向建立空间直角坐标系,利用同量法能求出SN与平面DMN所成角的余弦值.
解答 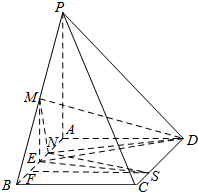 证明:(1)如图,取AB中点E,连接EM、ED,…(1分)
证明:(1)如图,取AB中点E,连接EM、ED,…(1分)
∵M为PB中点,所以EM∥PA…(2分)
又PA⊥面ABCD,SN?面ABCD,
∴PA⊥SN,所以EM⊥SN…(3分)
∵$AD=\frac{1}{2}AB=AE$,所以∠AED=45°…(4分)
过S作SF⊥AB交AB于F则NF=FS,∴∠FNS=45°
∴ES⊥ED…(5分)又ED∩ME=E,SN⊥平面EDM
∴SN⊥DM…(6分)
解:设PA=1,以A为原点,射线AB,AD,AP分别为x,y,z轴正方向建立空间直角坐标系,
则P(0,0,1),D(0,1,0),$M(1,0,\frac{1}{2})$,$N(\frac{1}{2},0,0)$,$S(\frac{3}{2},1,0)$…(7分)
$\overrightarrow{DM}=(1,-1,\frac{1}{2})$,$\overrightarrow{SN}=(-1,-1,0)$,$\overrightarrow{DN}=(\frac{1}{2},-1,0)$,
设$\overrightarrow n=(x,y,z)$为平面DMN的一个法向量,
则$\left\{\begin{array}{l}\overrightarrow{DM}•\overrightarrow n=0\\ \overrightarrow{DN}•\overrightarrow n=0\end{array}\right.$,∴$\left\{\begin{array}{l}x-y+\frac{1}{2}z=0\\ \frac{1}{2}x-y=0\end{array}\right.$…(8分)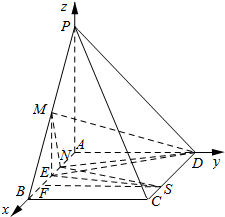
取x=2,得$\overrightarrow n=(2,1,-2)$…(9分)
设SN与平面DMN所成角为α
∴$sinα=|cos<\overrightarrow{SN},\overrightarrow n>|=\frac{|-2-1-0|}{{\sqrt{2}•\sqrt{9}}}=\frac{{\sqrt{2}}}{2}$…(10分)
∴$cosα=\frac{{\sqrt{2}}}{2}$…(11分)
∴SN与平面DMN所成角的余弦值为$\frac{{\sqrt{2}}}{2}$.…(12分)
点评 本题考查线线垂直、线面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
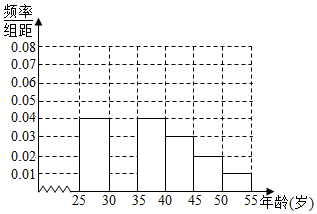 某校学生利用元旦节进行社会实践,在[25,55]岁的人群随机抽取n人,进行了一次“是否已养成垃圾分类习惯”的调查,得到如下统计表和各年龄段人数频率分布直方图:
某校学生利用元旦节进行社会实践,在[25,55]岁的人群随机抽取n人,进行了一次“是否已养成垃圾分类习惯”的调查,得到如下统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 已养成垃圾分类习惯的人数 | 占本组频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六祖 | [50,55] | 15 | 0.3 |
(Ⅱ)从[40,50)岁年龄段的“已养成垃圾分类习惯的人”中采用分层抽样法抽取6人参加垃圾分类宣讲活动,其中选取2人作为领队,求选取的2名领队年龄都在[40,45)岁的概率.
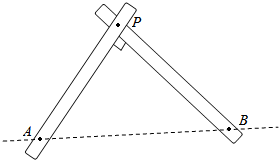 如图所示,两根杆分别绕着点A和B(AB=2a)在平面内转动,并且转动时两杆保持互相垂直,求杆的交点P的轨迹方程.
如图所示,两根杆分别绕着点A和B(AB=2a)在平面内转动,并且转动时两杆保持互相垂直,求杆的交点P的轨迹方程.