某几何体的三视图如图所示.方格纸中小正方形的边长为1.则此几何体的体积为( )A．$\frac{4}{3}$B．$\frac{2}{3}$C．2D．4 题目和参考答案——青夏教育精英家教网—

题目内容

13．某几何体的三视图如图所示，方格纸中小正方形的边长为1，则此几何体的体积为（　　）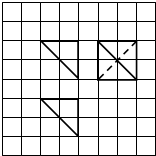

A．

$\frac{4}{3}$

B．

$\frac{2}{3}$

C．

D．

分析画出满足条件的几何体的直观图，代入棱锥体积，可得答案．

解答解：由已知中的三视图可得该几何体是一个三棱锥，其直观图如下图所示：

故几何体的体积V=$\frac{1}{3}$×（$\frac{1}{2}$×2×2）×2=$\frac{4}{3}$，
故选：A

点评本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．

练习册系列答案

4．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=3，且$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影与$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影相等，则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于$\sqrt{10}$．

1．

如图所示，正方体ABCD-A′B′C′D′的棱长为1，E、F分别是棱AA′，CC′的中点，过直线E，F的平面分别与棱BB′、DD′交于M、N，设BM=x，x∈（0，1），给出以下四个命题：
①四边形MENF为平行四边形；
②若四边形MENF面积s=f（x），x∈（0，1），则f（x）有最小值；
③若四棱锥A-MENF的体积V=p（x），x∈（0，1），则p（x）为常函数；
④若多面体ABCD-MENF的体积V=h（x），x∈（$\frac{1}{2}$，1），则h（x）为单调函数；
其中假命题为（　　）

8．求（x-$\frac{1}{x}$）¹⁰的二项展开式中含有x²的项．

18．己知α是第三象限角，且tanα=$\frac{5}{12}$，则cosα的值是（　　）

5．设$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是空间两个不共线的向量，已知$\overrightarrow{AB}$=$\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$，$\overrightarrow{BC}$=5$\overrightarrow{{e}_{1}}$+4$\overrightarrow{{e}_{2}}$，$\overrightarrow{DC}$=-$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$，且A，B，D三点共线，则实数k=1．

2．下列条件使M与A，B，C一定共面的是（　　）

	A．	$\overrightarrow{OM}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$+$\overrightarrow{OC}$		B．	$\overrightarrow{OM}$+$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$
	C．	$\overrightarrow{OM}$=$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$		D．	$\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=$\overrightarrow{0}$

3．如图，直线l经过第二、第三、第四象限，l的倾斜角为α，斜率为k，则（　　）

试题分类