题目内容
（文）已知定点A（4，0）和圆x2+y2=4上的动点B，点P（x，y）是线段AB的中点，则点P的轨迹方程为 ．
考点：轨迹方程
专题：计算题,直线与圆
分析：设出P，B的坐标，确定动点之间坐标的关系，利用端点B在圆x2+y2=4上运动，可得轨迹方程．
解答：
解：设线段AB中点为P（x，y），B（m，n），则m=2x-4，n=2y
∵端点B在圆x2+y2=4上运动，
∴m2+n2=4
∴（2x-4）2+（2y）2=4
∴（x-2）2+y2=1．
故答案为：（x-2）2+y2=1．
∵端点B在圆x2+y2=4上运动，
∴m2+n2=4
∴（2x-4）2+（2y）2=4
∴（x-2）2+y2=1．
故答案为：（x-2）2+y2=1．
点评：本题考查轨迹方程，考查代入法的运用，确定动点之间坐标的关系是关键．
练习册系列答案
一线名师提优试卷系列答案
相关题目
已知空间上的两点A（-1，2，1）、B（-2，0，3），以AB为体对角线构造一个正方体，则该正方体的体积为（ ）
| A、3 | ||
B、2
| ||
| C、9 | ||
D、3
|
已知a，b，c∈R，给出下列命题：
①若a＞b，则ac2＞bc2；
②若ab≠0，则
+
≥2；
③若a＞b＞0，n∈N*，则an＞bn；
④若logab＜0（a＞0，a≠1），则a，b中至少有一个大于1．
其中真命题的个数为（ ）
①若a＞b，则ac2＞bc2；
②若ab≠0，则
| a |
| b |
| b |
| a |
③若a＞b＞0，n∈N*，则an＞bn；
④若logab＜0（a＞0，a≠1），则a，b中至少有一个大于1．
其中真命题的个数为（ ）
| A、2 | B、3 | C、4 | D、1 |
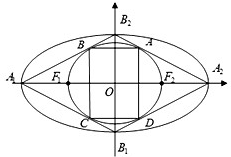如图，椭圆| x2 |
| a2 |
| y2 |
| b2 |
| S1 |
| S2 |
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
已知向量
=（3，1），
=（x，-2），
=（0，2），若
⊥（
-
），则实数x的值为（ ）
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||
B、
| ||
C、-
| ||
D、-
|