题目内容
已知定义域为R的奇函数y=f(x)的导函数为y=f′(x),当x≠0时,f′(x)+
>0,若a=
f(
),b=-2f(-2),c=(ln
)f(ln
),则a,b,c的大小关系正确的是( )
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、b<c<a |
| C、a<c<b |
| D、c<a<b |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:利用条件构造函数h(x)=xf(x),然后利用导数研究函数h(x)的单调性,利用函数的单调性比较大小.
解答:
解:设h(x)=xf(x),
∴h′(x)=f(x)+x•f′(x),
∵y=f(x)是定义在实数集R上的奇函数,
∴h(x)是定义在实数集R上的偶函数,
当x>0时,h'(x)=f(x)+x•f′(x)>0,
∴此时函数h(x)单调递增.
∵a=
f(
)=h(
),b=-2f(-2)=2f(2)=h(2),
c=(ln
)f(ln
)=h(ln
)=h(-ln2)=h(ln2),
又2>ln2>
,
∴b>c>a.
故选:C.
∴h′(x)=f(x)+x•f′(x),
∵y=f(x)是定义在实数集R上的奇函数,
∴h(x)是定义在实数集R上的偶函数,
当x>0时,h'(x)=f(x)+x•f′(x)>0,
∴此时函数h(x)单调递增.
∵a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
c=(ln
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又2>ln2>
| 1 |
| 2 |
∴b>c>a.
故选:C.
点评:本题考查如何构造新的函数,利用单调性比较大小,是常见的题目.本题属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
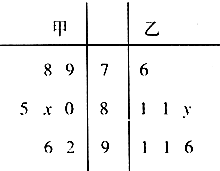 某中学高一年级从甲、乙两个班级各选出7名学生参加学科测试,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.
某中学高一年级从甲、乙两个班级各选出7名学生参加学科测试,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83. 如图,AD、BE是△ABC的两条高,求证:∠CED=∠ABC.
如图,AD、BE是△ABC的两条高,求证:∠CED=∠ABC.