题目内容
已知函数f(x)=|2x+1|-|x|-2
(Ⅰ)解不等式f(x)≥0
(Ⅱ)若存在实数x,使得f(x)≤|x|+a,求实数a的取值范围.
(Ⅰ)解不等式f(x)≥0
(Ⅱ)若存在实数x,使得f(x)≤|x|+a,求实数a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)化简函数的解析式,分类讨论,求得不等式的解集.
(Ⅱ)不等式即|x+
|-|x|≤
+1①,由题意可得,不等式①有解.根据绝对值的意义可得|x+
|-|x|∈[-
,
],故有
+1≥-
,由此求得a的范围.
(Ⅱ)不等式即|x+
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)函数f(x)=|2x+1|-|x|-2=
,
当x<-
时,由-x-3≥0,可得x≤-3.
当-
≤x<0时,由3x-1≥0,求得 x∈∅.
当x≥0时,由x-1≥0,求得 x≥1.
综上可得,不等式的解集为{x|x≤-3 或x≥1}.
(Ⅱ)f(x)≤|x|+a,即|x+
|-|x|≤
+1①,由题意可得,不等式①有解.
由于|x+
|-|x|表示数轴上的x对应点到-
对应点的距离减去它到原点的距离,故|x+
|-|x|∈[-
,
],
故有
+1≥-
,求得a≥-3.
|
当x<-
| 1 |
| 2 |
当-
| 1 |
| 2 |
当x≥0时,由x-1≥0,求得 x≥1.
综上可得,不等式的解集为{x|x≤-3 或x≥1}.
(Ⅱ)f(x)≤|x|+a,即|x+
| 1 |
| 2 |
| a |
| 2 |
由于|x+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故有
| a |
| 2 |
| 1 |
| 2 |
点评:本题主要考查绝对值的意义,绝对值不等式的解法,函数的能成立问题,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设
,
是单位向量,则“
•
>0”是“
和
的夹角为锐角”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
中小学校车安全引起社会的关注,为了彻底消除校车安全隐患,某市购进了50台完全相同的校车,准备发放给10所学校,每所学校至少2台,则不同的发放方案种数为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知g(x)=ax+1,f(x)=
,对?x1∈[-2,2],?x2∈[-2,2].,使g(x1)=f(x2)成立,则a的取值范围是( )
|
| A、[-1,+∞) |
| B、[-1,1] |
| C、(0,1] |
| D、(-∞,1] |
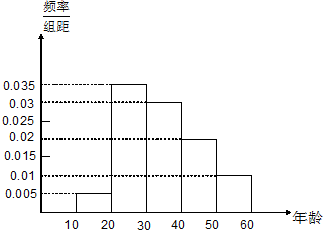 某班同学利用寒假进行社会实践,对年龄段在[10,60]的人生活习惯是否符合环保理念进行调查,现随机抽取n人进行数据分析,得到如下频率分布表和频率分布直方图;
某班同学利用寒假进行社会实践,对年龄段在[10,60]的人生活习惯是否符合环保理念进行调查,现随机抽取n人进行数据分析,得到如下频率分布表和频率分布直方图;