题目内容
17.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递增区间为( )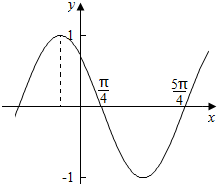
| A. | (kπ+$\frac{3}{4}$π,kπ+$\frac{7}{4}$π),k∈Z | B. | (kπ+$\frac{π}{4}$,kπ+$\frac{5π}{4}$),k∈Z | ||
| C. | (2kπ+$\frac{π}{4}$,2kπ+$\frac{5}{4}$π),k∈Z | D. | (2k+$\frac{3}{4}$π,2k+$\frac{7}{4}$π),k∈Z |
分析 根据三角函数的图象求出函数的解析式,结合三角函数的单调性进行求解即可.
解答 解:函数的周期T=2×($\frac{5π}{4}$π-$\frac{π}{4}$)=2π,即$\frac{2π}{ω}=π$,得ω=1,
则f(x)=cos(x+φ),
则当x=$\frac{\frac{π}{4}+\frac{5π}{4}}{2}$=$\frac{3}{4}$π时,函数取得最小值,
则$\frac{3}{4}$π+φ=π+2kπ,即φ=$\frac{π}{4}$+2kπ,
即f(x)=cos(x+$\frac{π}{4}$),
由2kπ+π<x+$\frac{π}{4}$<2kπ+2π,k∈Z,
即2k+$\frac{3}{4}$π<x<2k+$\frac{7}{4}$π,k∈Z,
即函数的单调递增区间为为(2k+$\frac{3}{4}$π,2k+$\frac{7}{4}$π),
故选:D
点评 本题主要考查三角函数解析式和单调区间的求解,根据图象求出函数的解析式是解决本题的关键.

练习册系列答案
相关题目
20.过椭圆4x2+2y2=1的一个焦点F1的直线与椭圆相交于A、B两点,则A、B与椭圆的另一个焦点F2构成的△ABF2的周长等于( )
| A. | 2 | B. | 4 | C. | 8 | D. | 2$\sqrt{2}$ |
5.坐标平面上的点集S满足S=$\{(x,y)|{log_2}({y^2}-y+2)=2{sin^4}x+2{cos^4}x,-\frac{π}{8}≤x≤\frac{π}{4}\}$,将点集S中的所有点向y轴作投影,所得投影线段的总长度为( )
| A. | 1 | B. | $\frac{{\sqrt{3}+\sqrt{5}}}{2}$ | C. | $\sqrt{8\sqrt{2}-7}$ | D. | 2 |
12.设i是虚数单位,复数$\frac{4i}{1+i}$=( )
| A. | 2-2i | B. | -2-2i | C. | -2+2i | D. | 2+2i |
2.已知A是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点,点P的坐标为(0,a),若线段AP的中点Q在椭圆上,则椭圆的离心率e为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
9.已知2a=3b=m,ab≠0且a,ab,b成等差数列,则m=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 6 |