题目内容
11. A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.
A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.(1)若A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),求$\frac{2sinα•sinα}{co{s}^{2}α+1-2si{n}^{2}α}$的值;
(2)求|BC|2的取值范围.
分析 (1)根据点A的坐标,得出sinα与cosα的值,代入计算即可;
(2)用α表示出∠BOC,再利用余弦定理写出|BC|2的表达式,求出它的取值范围即可.
解答 解:(1)∵A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),
∴sinα=$\frac{4}{5}$,cosα=$\frac{3}{5}$;
∴$\frac{2sinα•sinα}{co{s}^{2}α+1-2si{n}^{2}α}$=$\frac{2×\frac{4}{5}×\frac{3}{5}}{{(\frac{3}{5})}^{2}+1-2{×(\frac{4}{5})}^{2}}$=12;
(2)∵∠AOC=α,α∈(0,$\frac{π}{2}$),
∴∠BOC=α+$\frac{π}{2}$;
∴|BC|2=|OB|2+|OC|2-2|OB|•|OC|cos∠BOC
=1+1-2cos(α+$\frac{π}{2}$)=2+2sinα,
又α∈(0,$\frac{π}{2}$),
∴sinα∈(0,1),
∴2+2sinα∈(2,4),
即|BC|2的取值范围是(2,4).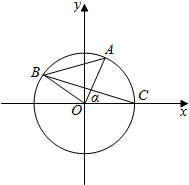
点评 本题考查了三角函数的定义与三角函数式的化简求值问题,也考查了余弦定理的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.对于任意的整数n(n≥2),满足an=a+1,b2n=b+3a的正数a和b的大小关系是( )
| A. | a>b>1 | B. | b>a>1 | C. | a>1,0<b<1 | D. | 0<a<1,b>1 |
19.cos(-$\frac{26π}{3}$)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
6.若实数x,y满足$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,则z=$\sqrt{{x}^{2}+{y}^{2}}$的最大值是( )
| A. | $\sqrt{43}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | $\sqrt{73}$ | D. | 3$\sqrt{2}$ |
3.若(x-1)100=a0x100+a1x99+…+a100对一切实数x恒成立,则a3+a97的值为( )
| A. | 0 | B. | C${\;}_{100}^{3}$ | C. | -2C${\;}_{100}^{3}$ | D. | 2100 |
20.过椭圆4x2+2y2=1的一个焦点F1的直线与椭圆相交于A、B两点,则A、B与椭圆的另一个焦点F2构成的△ABF2的周长等于( )
| A. | 2 | B. | 4 | C. | 8 | D. | 2$\sqrt{2}$ |
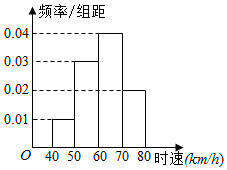 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论: