题目内容
已知等差数列{an}的前21项和S21=189，则a11= ．
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的性质和求和公式可得S21=21a11=189，解方程可得．
解答：
解：由题意可得S21=
（a1+a21）=189，
又由等差数列的性质可得2a11=a1+a21，
∴S21=21a11=189，
解得a11=9
故答案为：9
| 21 |
| 2 |
又由等差数列的性质可得2a11=a1+a21，
∴S21=21a11=189，
解得a11=9
故答案为：9
点评：本题考查等差数列的求和公式和性质，属基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
已知向量
，
分别是直线l和平面α的方向向量和法向量，若cos＜
，
＞=-
，则l与α所成的角为（ ）
| m |
| n |
| m |
| n |
| 1 |
| 2 |
| A、30° | B、60° |
| C、120° | D、150° |
设a，b是两条不同的直线，α，β是两个不同的平面，a?α，b⊥β，则α∥β是a⊥b的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、即非充分又非必要条件 |
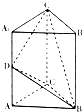如图，在直三棱柱ABC-A1B1C1中，AC=BC=