题目内容
12.已知数列{an},${a_n}=\left\{\begin{array}{l}n+1,n≤7\\ n-1,n>7\end{array}\right.(n∈{N^*})$.(1)判断数列{an}是否为等差数列;
(2)求数列{an}的前n项和Sn.
分析 (1)利用等差数列的定义,反例判断即可.
(2)通过数列的项数分别求解数列的和即可.
解答 解:(1)a2-a1=1,a8-a7=7-8=-1,数列不是等差数列.…(1分)
(2)解:①当n≤7时,${S_n}=2n+\frac{n(n-1)}{2}×1$=$\frac{n^2}{2}+\frac{3n}{2}$.
②当n>7时,${S_n}=35+\frac{(n-1)[7+(n-1)]}{2}$=$35+\frac{(n-7)(n+6)}{2}$=$\frac{{{n^2}-n}}{2}+14$.…(5分)
点评 本题考查数列求和,等差数列的判断,考查计算能力.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
7.如果关于x的不等式x2<ax+b的解集是{x|1<x<3},那么ba等于( )
| A. | -81 | B. | 81 | C. | -64 | D. | 64 |
4.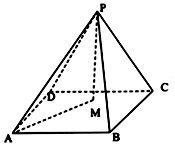 四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )
四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )
 四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )
四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )| A. | 一个点 | B. | 线段 | C. | 圆 | D. | 圆弧 |
1.某风险投资公司选择了三个投资项目,设每个项目成功的概率都为$\frac{1}{2}$,且相互之间设有影响,若每个项目成功都获利20万元,若每个项目失败都亏损5万元,该公司三个投资项目获利的期望为( )
| A. | 30万元 | B. | 22.5万元 | C. | 10万元 | D. | 7.5万元 |
2.定义在R上的函数f(x)满足f'(x)-f(x)=x•ex,且$f(0)=\frac{1}{2}$,则$\frac{{x•{e^x}}}{f(x)}$的最大值为( )
| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1 | D. | 0 |