Question

4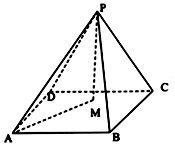．四棱锥P-ABCD中，△PCD为正三角形，底面边长为1的正方形，平面PCD⊥平面ABCD，M为底面内一动点，当$MA=\sqrt{2}PM$时，点M在底面正方形内（包括边界）的轨迹为（　　）

• A． 一个点
• B． 线段
• C． 圆
• D． 圆弧

Answer 1

分析 由题意，建立如图所示的坐标系，利用$MA=\sqrt{2}PM$，得出M的轨迹方程，即可得出结论．

解答 解：由题意，建立如图所示的坐标系，A（1，-$\frac{1}{2}$，0），P（0，0，$\frac{\sqrt{3}}{2}$），
设M（x，y，0）
∵$MA=\sqrt{2}PM$，
∴（x-1）²+（y+$\frac{1}{2}$）²=2（x²+y²+$\frac{3}{4}$），
∴x²+y²+2x-y+$\frac{1}{4}$=0，表示圆．
故选C．

点评 本题考查棱锥的结构特征，考查学生的计算能力，属于中档题．