题目内容
17.四面体ABCD中,已知AB=AC=BC=BD=CD=1,则该四面体体积的最大值是$\frac{1}{8}$,表面积的最大值是$\frac{\sqrt{3}}{2}$+1.分析 当平面ABC⊥平面BDC时,该四体体积最大;当AC⊥CD,AB⊥BD时,该四面体表面积取最大值.
解答 解: ∵四面体ABCD中,AB=AC=BC=BD=CD=1,
∵四面体ABCD中,AB=AC=BC=BD=CD=1,
∴当平面ABC⊥平面BDC时,该四体体积最大,
此时,过D作DE⊥平面ABC,交BC于E,连结AE,
则AE=DE=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
∴该四面体体积的最大值:
Smax=$\frac{1}{3}×\frac{1}{2}×1×\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}$=$\frac{1}{8}$.
∵△ABC,△BCD都是边长为1的等边三角形,
面积都是S=$\frac{1}{2}×1×1×sin60°$=$\frac{\sqrt{3}}{4}$,
∴要使表面积最大需△ABD,△ACD面积最大,
∴当AC⊥CD,AB⊥BD时,表面积取最大值,
此时${S}_{△ADC}={S}_{{\;}_{△}ABC}$=$\frac{1}{2}×1×1=\frac{1}{2}$,
四面体表面积最大值Smax=$\frac{1}{2}+\frac{1}{2}+\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}$=1+$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{1}{8}$,$\frac{\sqrt{3}}{2}+1$.
点评 本题考查四面体的体积的最大值和表面积最大值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
8.已知向量$\vec a,\vec b$,那么$\frac{1}{2}(2\vec a-4\vec b)+2\vec b$等于( )
| A. | $\vec a-2\vec b$ | B. | $\overrightarrow{a}$-4$\vec b$ | C. | $\vec a$ | D. | $\vec b$ |
5.如果圆C:(x-a)2+(y-3)2=5的一条切线的方程为y=2x,那么a的值为( )
| A. | 4或1 | B. | -1或4 | C. | 1或-4 | D. | -1或-4 |
2.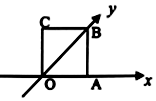 如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )
如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )
 如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )
如图水平放置的一个平面图形的直观图是边长为1cm的正方形,则原图形的周长是( )| A. | 8cm | B. | 6cm | C. | $2(1+\sqrt{3})cm$ | D. | $2(1+\sqrt{2})cm$ |
7.从1,2,3,4,5,6,7中任取两个不同的数,事件A为“取到的两个数的和为偶数”,事件B为“取到的两个数均为奇数”则P(B|A)=( )
| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
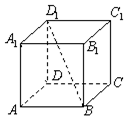 如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,
如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,