题目内容
1.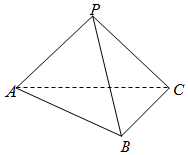 如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.
如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.(Ⅰ)求证:AC⊥PB;
(Ⅱ)若点M在棱BC上,且二面角M-PA-C的余弦值为$\frac{3\sqrt{11}}{11}$,求BM的长.
分析 (Ⅰ)取AC中点O,连结OB,OP,可得OB⊥AC,OP⊥AC,即可证得AC⊥面POB,即AC⊥PB.
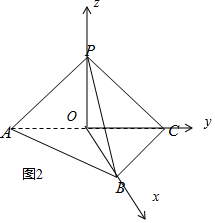
(Ⅱ)以O为坐标原点,OB、OC、OP分别为x、y、z轴建立如图(2)所示空间直角坐标系.因为$AB=BC=AP=PC=\sqrt{2}$,∠ABC=∠APC=90°,所以OB=OC=OP=1,从而O(0,0,0),A(0,-1,0),B(1,0,0),C(0,1,0),P(0,0,1),利用向量法求解.
解答 解:(Ⅰ)如图(1)取AC中点O,连结OB,OP
因为AB=BC,所以OB⊥AC,
因为AP=PC,所以OP⊥AC,∵OB∩OP=O,
∴AC⊥面POB∵PB?面POB∴AC⊥PB…(4分)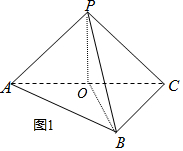
(Ⅱ)∵平面ABC⊥平面APC,平面ABC∩平面APC=AC,
由(Ⅰ)可知OP⊥AC,∴OP⊥平面ABC,∵OB?平面ABC,∴OB⊥OP
以O为坐标原点,OB、OC、OP分别为x、y、z轴建立如图(2)所示空间直角坐标系.
因为$AB=BC=AP=PC=\sqrt{2}$,∠ABC=∠APC=90°,所以OB=OC=OP=1,
从而O(0,0,0),A(0,-1,0),B(1,0,0),C(0,1,0),P(0,0,1),…(6分)
由题意可得:$\overrightarrow{n_1}=\overrightarrow{OB}=(1,0,0)$是平面PAC的一个法向量,
设$\overrightarrow{BM}=λ\overrightarrow{BC}(0≤λ<1)$,M(m,n,0)
由$\overrightarrow{BM}=(m-1,n,0)$,$\overrightarrow{BC}=(-1,1,0)$,得:m=1-λ,n=λ,∴M(1-λ,λ,0)…(8分)
设平面PAM的法向量为$\overrightarrow{n_2}=(x,y,z)$,
则$\overrightarrow{AP}=(0,1,1)$,$\overrightarrow{AM}=(1-λ,λ+1,0)$,
由$\left\{{\begin{array}{l}{\overrightarrow{AP}•\overrightarrow{n_2}=0}\\{\overrightarrow{AM}•\overrightarrow{n_2}=0}\end{array}}\right.$⇒$\left\{{\begin{array}{l}{y+z=0}\\{(1-λ)x+(λ+1)y=0}\end{array}}\right.$,
令z=1,则y=-1,$x=\frac{1+λ}{1-λ}$,∴$\overrightarrow{n_2}=(\frac{1+λ}{1-λ},-1,1)$…(10分)
设二面角M-PA-C的平面角为θ,
则$cosθ=cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}|•|\overrightarrow{n_2}|}}=\frac{{\frac{1+λ}{1-λ}}}{{\sqrt{{{(\frac{1+λ}{1-λ})}^2}+2}}}=\frac{{3\sqrt{11}}}{11}$,
∴$λ=\frac{1}{2}$∴$\overrightarrow{BM}=\frac{1}{2}\overrightarrow{BC}$,∴$BM=\frac{1}{2}BC=\frac{{\sqrt{2}}}{2}$…(12分)
点评 本题考查了空间线线垂直,向量法处理二面角的运算,属于中档题.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案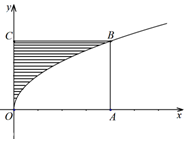 如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
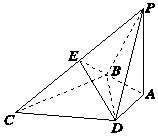 如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC. 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.