题目内容
7.已知等差数列{an}的公差为d,前n项和为Sn,则“d>0”是“S4+S6>2S5”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据等差数列的求和公式和S4+S6>2S5,可以得到d>0,根据充分必要条件的定义即可判断.
解答 解:∵S4+S6>2S5,
∴4a1+6d+6a1+15d>2(5a1+10d),
∴21d>20d,
∴d>0,
故“d>0”是“S4+S6>2S5”充分必要条件,
故选:C
点评 本题借助等差数列的求和公式考查了充分必要条件,属于基础题

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
15.若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是( )
| A. | f(x)=2-x | B. | f(x)=x2 | C. | f(x)=3-x | D. | f(x)=cosx |
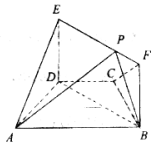 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.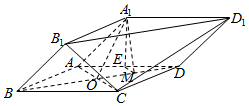 由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,
由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,