题目内容
若复数z满足z=i（2+4i）（i是虚数单位），则在复平面内，z对应的点的坐标是（ ）
| A、（-4，2） |
| B、（-2，4） |
| C、（2，4） |
| D、（4，2） |
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：直接利用复数的乘法运算化简复数z为a+bi（a，b∈R）的形式，则答案可求．
解答：
解：z=i（2+4i）=-4+2i．
∴在复平面内，z对应的点的坐标是（-4，2）．
故选：A．
∴在复平面内，z对应的点的坐标是（-4，2）．
故选：A．
点评：本题考查了复数的代数表示法及其几何意义，考查了复数的乘法运算，是基础题．
练习册系列答案
相关题目
下列结论错误的是（ ）
| A、命题“若p，则q”与命题“若非q，则非p”互为逆否命题 | ||||||
B、“sinx=
| ||||||
C、为得到函数y=sin（2x-
| ||||||
D、命题q：?x∈R，sinx-cosx≤
|
下列古典概型的说法中正确的个数是（ ）
①试验中所有可能出现的基本事件只有有限个；
②每个事件出现的可能性相等；
③基本事件的总数为n，随机事件A包含k个基本事件，则P（A）=
；
④每个基本事件出现的可能性相等．
①试验中所有可能出现的基本事件只有有限个；
②每个事件出现的可能性相等；
③基本事件的总数为n，随机事件A包含k个基本事件，则P（A）=
| k |
| n |
④每个基本事件出现的可能性相等．
| A、1 | B、2 | C、3 | D、4 |
在△ABC中，如果a，b，c分别是角A，B，C的对边，设命题p：（a2+b2）sin（A-B）=（a2-b2）sin（A+B）；命题q：△ABC为直角三角形，那么命题p是命题q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
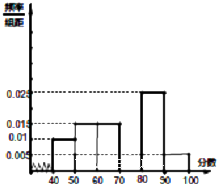某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段[40，50），[50，60），[90，100]后画出如下部分频率颁布直方图，观察图形的信息，回答下列问题：
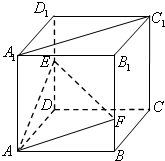如图，在棱长为a的正方体ABCD-A1B1C1D1中，点E是棱D1D的中点，点F在棱B1B上，且满足B1F=2FB．