题目内容
5.已知数列{an}的前n项和为Sn,且满足Sn=2an-2;数列{bn}的前n项和为Tn,且满足b1=1,b2=2,$\frac{T_n}{{{T_{n+1}}}}=\frac{b_n}{{{b_{n+2}}}}$.(1)求数列{an}、{bn}的通项公式;
(2)是否存在正整数n,使得$\frac{{{a_n}+{b_n}+1}}{{{a_n}-{b_{n+1}}}}$恰为数列{bn}中的一项?若存在,求所有满足要求的bn;若不存在,说明理由.
分析 (1)由当n≥2时,Sn-1=2an-1-2,an=Sn-Sn-1,即可求得an=2an-1,则数列{an}是以2为首项,2为公比的等比数列;由$\frac{T_n}{{{T_{n+1}}}}=\frac{b_n}{{{b_{n+2}}}}$.采用“累乘法”即可求得当n≥2时,bn+1-bn-1=2,数列{bn}的奇数项,偶数项分别成立等差数列,b3=T2=b1+b2=3,b1+b3=2b2,数列{bn}是以b1=1为首项,1为公差的等差数列,即可求得数列{an}、{bn}的通项公式;
(2)设cn=$\frac{{{a_n}+{b_n}+1}}{{{a_n}-{b_{n+1}}}}$=$\frac{{2}^{n}+n+1}{{2}^{n}-(n+1)}$,作差比较大小,cn>cn+1>1,根据数列的单调性,即可求得存在n=2,使得b7=c2,b3=c3.
解答 解:(1)由Sn=2an-2,则当n≥2时,Sn-1=2an-1-2,
两式相减得:an=2an-2an-1,则an=2an-1,
由S1=2a1-2,则a1=2,
∴数列{an}是以2为首项,2为公比的等比数列,则an=2n,
由$\frac{T_n}{{{T_{n+1}}}}=\frac{b_n}{{{b_{n+2}}}}$.
则$\frac{{T}_{1}}{{T}_{2}}$=$\frac{{b}_{1}}{{b}_{3}}$,$\frac{{T}_{2}}{{T}_{3}}$=$\frac{{b}_{2}}{{b}_{4}}$,$\frac{{T}_{3}}{{T}_{4}}$=$\frac{{b}_{3}}{{b}_{5}}$,…,$\frac{{T}_{n-1}}{{T}_{n}}$=$\frac{{b}_{n-1}}{{b}_{n+1}}$.$\frac{{T}_{n}}{{T}_{n+1}}$=$\frac{{b}_{n}}{{b}_{n+2}}$
以上各式相乘,$\frac{{T}_{1}}{{T}_{n+1}}$=$\frac{{b}_{1}{b}_{2}}{{b}_{n+1}{b}_{n+2}}$,则2Tn=bnbn+1,
当n≥2时,2Tn-1=bn-1bn,两式相减得:2bn=bn(bn+1-bn-1),即bn+1-bn-1=2,
∴数列{bn}的奇数项,偶数项分别成等差数列,
由$\frac{{T}_{1}}{{T}_{2}}$=$\frac{{b}_{1}}{{b}_{3}}$,则b3=T2=b1+b2=3,b1+b3=2b2,
∴数列{bn}是以b1=1为首项,1为公差的等差数列,
∴数列{bn}的通项公式bn=n;
(2)当n=1时,$\frac{{{a_n}+{b_n}+1}}{{{a_n}-{b_{n+1}}}}$无意义,
设cn=$\frac{{{a_n}+{b_n}+1}}{{{a_n}-{b_{n+1}}}}$=$\frac{{2}^{n}+n+1}{{2}^{n}-(n+1)}$,(n≥2,n∈N*),
则cn+1-cn=$\frac{{2}^{n+1}+n+2}{{2}^{n+1}-(n+2)}$-$\frac{{2}^{n}+n+1}{{2}^{n}-(n+1)}$=$\frac{-n•{2}^{n+1}}{[{2}^{n+1}-(n+2)][{2}^{n}-(n+1)]}$<0,
即cn>cn+1>1,
显然2n+n+1>2n-(n+1),则c2=7>c3=3>c4>…>1,
∴存在n=2,使得b7=c2,b3=c3,
下面证明不存在c2=2,否则,cn=$\frac{{2}^{n}+n+1}{{2}^{n}-(n+1)}$=2,即2n=3(n+1),
此时右边为3的倍数,而2n不可能是3的倍数,故该不等式成立,
综上,满足要求的bn为b3,b7.
点评 本题考查数列的综合应用,考查等比数列及等差数列的通项公式及证明,考查数列单调性的判断,考查转化思想,属于难题.

| A. | y=sinx | B. | y=sin2|x| | C. | y=-cos2x | D. | y=cos2x |
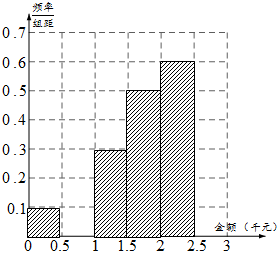 某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):
某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):| 网购金额 (单位千元) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
(1)试确定x,y,p,q的值,并补全频率分布直方图;
(2)试营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定5人,若需从这5人中随机选取2人进行问卷调查,则恰好选取1名“网购达人”和1名“非网购达人”的概率是多少?
| A. | i(1+i)2 | B. | i2(1-i) | C. | (1+i)2 | D. | i(1+i) |
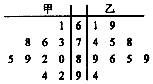 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如下图所示的茎叶图.规定模拟考试成绩不低于81分为优秀等次.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如下图所示的茎叶图.规定模拟考试成绩不低于81分为优秀等次.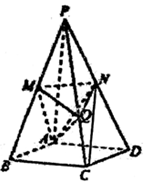 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分别为PB,PD的中点.