Question

13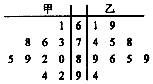．甲、乙两位同学参加数学竞赛培训，培训期间共参加了10次模拟考试，根据考试成绩，得到如下图所示的茎叶图．规定模拟考试成绩不低于81分为优秀等次．
（1）求乙学生的平均成绩及方差；
（2）从甲学生的10次模拟考试成绩中随机选取3个，记成绩为优秀等次的个数为X，求X的分布列和数学期望．

Answer 1

分析 （1）由茎叶图能求出乙学生的平均成绩和方差．
（2）X的可能取值为0，1，2，3，分别求出相应的概率，由此能求出X的分布列和EX．

解答 解：（1）由茎叶图得乙学生的平均成绩为：
$\overline{x}$=$\frac{1}{10}$（61+69+74+75+78+89+86+89+94）=80，
方差为：
S²=$\frac{1}{10}$[（-19）²+（-11）²+（-6）²+（-5）²+（-2）²+9²+6²+5²+9²+14²]=96.6．
（2）X的可能取值为：
P（X=0）=$\frac{{C}_{5}^{0}{C}_{5}^{3}}{{C}_{10}^{3}}$=$\frac{1}{12}$，
P（X=1）=$\frac{{C}_{5}^{1}{C}_{5}^{2}}{{C}_{10}^{3}}$=$\frac{5}{12}$，
P（X=2）=$\frac{{C}_{5}^{1}{C}_{5}^{2}}{{C}_{10}^{3}}$=$\frac{5}{12}$，
P（X=3）=$\frac{{C}_{5}^{0}{C}_{5}^{3}}{{C}_{10}^{3}}$=$\frac{1}{12}$，
∴X的分布列为：

X	0	1	2	3
P	$\frac{1}{12}$	$\frac{5}{12}$	$\frac{5}{12}$	$\frac{1}{12}$

EX=$0×\frac{1}{12}+1×\frac{5}{12}+2×\frac{5}{12}+3×\frac{1}{12}$=1.5．

点评 本题考查概率的求法，考查离散型随机变量的分布列及数学期望的求法，涉及到平均数、方差、离散型随机变量的分布列及数学期望等知识点，考查推理论证能力、运算求解能力、数据处理能力，考查化归与转化思想，是中档题．