题目内容
20.已知$α-β=\frac{π}{3},tanα-tanβ=3$,则cos(α+β)的值为$\frac{\sqrt{3}}{3}-\frac{1}{2}$.分析 “切化弦”的思想,根据tanα-tanβ=$\frac{sinα}{cosα}-\frac{sinβ}{cosβ}=\frac{sin(α-β)}{cosαcosβ}$=3,α-β=$\frac{π}{3}$,求出cosαcosβ,在利用和与差求sinαsinβ,即可求cos(α+β)的值.
解答 解:tanα-tanβ=$\frac{sinα}{cosα}-\frac{sinβ}{cosβ}=\frac{sin(α-β)}{cosαcosβ}$=3,α-β=$\frac{π}{3}$,
∴cosαcosβ=$\frac{\sqrt{3}}{6}$.
cos(α-β)=cosαcosβ+sinαsinβ=$\frac{1}{2}$,
∴sinαsinβ=$\frac{1}{2}-\frac{\sqrt{3}}{6}$
那么:cos(α+β)=cosαcosβ-sinαsinβ=$\frac{\sqrt{3}}{3}-\frac{1}{2}$.
故答案为$\frac{\sqrt{3}}{3}-\frac{1}{2}$.
点评 本题考查了“切化弦”的思想和和与差的公式的灵活运用.考查了计算能力.属于中档题.

练习册系列答案
相关题目
10.为了考察某种药物治疗效果,进行动物试验,得到如下数据:
(1)求出表格中b,c,d的值;
(2)是否有95%的把握认为该药物有效.
附:
i:${k^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({a+d})({b+c})({b+d})}}$
ii:
| 患病 | 未患病 | 总计 | |
| 服用药 | 10 | b | 50 |
| 未服药 | c | d | 50 |
| 总计 | 30 | 70 | 100 |
(2)是否有95%的把握认为该药物有效.
附:
i:${k^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({a+d})({b+c})({b+d})}}$
ii:
| P(k2≥k) | 0.15 | 0.05 | 0.025 | 0.005 |
| k | 2.072 | 3.841 | 5.024 | 7.879 |
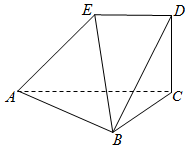 如图,AC=2ED,AC∥平面EDB,AC⊥平面BCD,平面ACDE⊥平面ABC.
如图,AC=2ED,AC∥平面EDB,AC⊥平面BCD,平面ACDE⊥平面ABC.