题目内容
将a,b都是整数的点(a,b)称为整点,若在圆x2+y2-6x+5=0内的整点中任取一点M,则点M到直线2x+y-12=0的距离大于
的概率为 .
| 5 |
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:首先化为标准方程,画出图象,找到满足条件的点,再根据点到直线距离公式,找到满足点M到直线2x+y-12=0的距离大于
的点,根据概率公式计算即可.
| 5 |
解答:
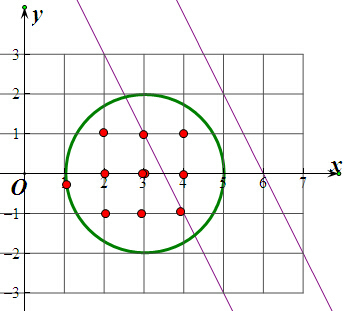 解:∵圆x2+y2-6x+5=0,即(x-3)2+y2=4内整数点有(2,1),(2,0),(2,-1),(3,1),(3,0),(3,-1),(4,1),(4,0),(4,-1)共9个,
解:∵圆x2+y2-6x+5=0,即(x-3)2+y2=4内整数点有(2,1),(2,0),(2,-1),(3,1),(3,0),(3,-1),(4,1),(4,0),(4,-1)共9个,
设点M(x,y),点M到直线2x+y-12=0的距离大于
,
∴
>
,
即|2x+y-12|>5,
即2x+y>17,或2x+y<7,
即y>17-2x,或y<7-2x,
则满足条的有其中(2,1),(2,0),(2,-1),(3,0),(3,-1)共5种,
故点M到直线2x+y-12=0的距离大于
的概率为P=
故答案为:
 解:∵圆x2+y2-6x+5=0,即(x-3)2+y2=4内整数点有(2,1),(2,0),(2,-1),(3,1),(3,0),(3,-1),(4,1),(4,0),(4,-1)共9个,
解:∵圆x2+y2-6x+5=0,即(x-3)2+y2=4内整数点有(2,1),(2,0),(2,-1),(3,1),(3,0),(3,-1),(4,1),(4,0),(4,-1)共9个,设点M(x,y),点M到直线2x+y-12=0的距离大于
| 5 |
∴
| |2x+y-12| | ||
|
| 5 |
即|2x+y-12|>5,
即2x+y>17,或2x+y<7,
即y>17-2x,或y<7-2x,
则满足条的有其中(2,1),(2,0),(2,-1),(3,0),(3,-1)共5种,
故点M到直线2x+y-12=0的距离大于
| 5 |
| 5 |
| 9 |
故答案为:
| 5 |
| 9 |
点评:本题考查圆的标准方程,点与直线的位置关系,得到满足条件的点的坐标,是解题的关键,属于基础题.

练习册系列答案
相关题目
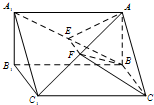 如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.