题目内容
已知a≤1,x∈(-∞,a],则函数f(x)=x2-2x+a的值( )
| A、[a-1,+∞) |
| B、[-a,+∞) |
| C、[a2-a,+∞) |
| D、[a2-1,+∞) |
考点:二次函数的性质
专题:函数的性质及应用
分析:先对函数配方,得出函数的单调区间,从而求出函数的值域.
解答:
解:f(x)=(x-1)2+a-1
开口向上,对称轴为x=1,
在区间(-∞,a]?(-∞,1]时,
函数单调递减,最小值为f(a)=a2-a,
所以f(x)的值域为[a2-a,+∞),
故选:C.
开口向上,对称轴为x=1,
在区间(-∞,a]?(-∞,1]时,
函数单调递减,最小值为f(a)=a2-a,
所以f(x)的值域为[a2-a,+∞),
故选:C.
点评:本题考查了二次函数的性质,考查了函数的单调性,是一道基础题.

练习册系列答案
相关题目
已知函数f(x)=x2+
,则“0<a<8”是“函数f(x)在(2,+∞)上为增函数”的( )
| a |
| x |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知△ABC内角A、B、C的对边分别是a、b、c,若cosB=
,b=2,sinC=2sinA,则△ABC的面积为( )
| 1 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
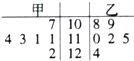 某质检机构检测某产品的质量是否合格,在甲乙两厂的匀速运行的自动包装传送带上每隔10分钟抽一包产品,称其质量(单位:克),分别记录抽查数据,获得质量数据茎叶图(如图).
某质检机构检测某产品的质量是否合格,在甲乙两厂的匀速运行的自动包装传送带上每隔10分钟抽一包产品,称其质量(单位:克),分别记录抽查数据,获得质量数据茎叶图(如图).