题目内容
已知函数f(x)的定义域为R,且在(0,+∞)上是单调增函数.
(1)若f(x)是R上的奇函数,x>0时,f(x)=x2+2x+3.求函数f(x)的解析式.
(2)若f(3a2-a+1)>f(a2+3a+7),求实数a的取值范围.
(1)若f(x)是R上的奇函数,x>0时,f(x)=x2+2x+3.求函数f(x)的解析式.
(2)若f(3a2-a+1)>f(a2+3a+7),求实数a的取值范围.
考点:二次函数的性质
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)由于f(x)是R上的奇函数,则当x=0时,f(0)=0,当x<0时,-x>0,利用已知解析式,结合奇函数,即可得到f(x)的表达式;
(2)由函数的单调性,得到二次不等式,解出即可.
(2)由函数的单调性,得到二次不等式,解出即可.
解答:
解:(1)由于f(x)是R上的奇函数,
则当x=0时,f(0)=0,
当x<0时,-x>0,则f(-x)=x2-2x+3,又f(-x)=-f(x),
则f(x)=-x2+2x-3,
则f(x)=
;
(2)由二次函数的对称轴和区间的关系可得,
x>0为增区间,x<0也为增区间,
f(x)在R上递增,
则f(3a2-a+1)>f(a2+3a+7),
即为3a2-a+1>a2+3a+7,
解得,a>3或a<-1.
则实数a的取值范围是(-∞,-1)∪(3,+∞).
则当x=0时,f(0)=0,
当x<0时,-x>0,则f(-x)=x2-2x+3,又f(-x)=-f(x),
则f(x)=-x2+2x-3,
则f(x)=
|
(2)由二次函数的对称轴和区间的关系可得,
x>0为增区间,x<0也为增区间,
f(x)在R上递增,
则f(3a2-a+1)>f(a2+3a+7),
即为3a2-a+1>a2+3a+7,
解得,a>3或a<-1.
则实数a的取值范围是(-∞,-1)∪(3,+∞).
点评:本题考查函数的奇偶性和单调性及运用,考查函数解析式的求法和不等式的解法,属于中档题.

练习册系列答案
相关题目
点P为椭圆
+
=1上一点,以点P以及焦点F1、F2为顶点的三角形的面积为1,则P点的坐标为( )
| x2 |
| 5 |
| y2 |
| 4 |
A、(±
| ||||
B、(
| ||||
C、(
| ||||
D、(±
|
过抛物线y2=2px(p>0)的焦点F作一直线l与抛物线交于P、Q两点,作PP1、QQ1垂直于抛物线的准线,垂足分别是P1、Q1,已知线段PF,QF的长度分别是4,9,那么|PQ1|=( )
| A、12 | ||
| B、13 | ||
C、4
| ||
| D、15 |
当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象为( )
A、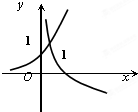 |
B、 |
C、 |
D、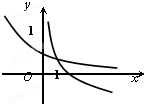 |