题目内容
已知⊙C:x2+y2=r2(r>0)和点P(a,b),若点P在⊙C上,求过点P且与⊙C相切的直线方程.
考点:圆的切线方程
专题:直线与圆
分析:点在圆上,找出圆心坐标,求出圆心与此点连线的斜率,确定出切线的斜率,写出切线方程即可.
解答:
解:点P(a,b)在圆x2+y2-4x=0上,
将圆化为标准方程得:a2+b2=r2,
∴圆心(0,0),半径为:r,
∵(a,b)与(0,0)连线的斜率为
,
∴切线的斜率为-
,
则切线方程为y-b=-
(x-a),即ax+by-r2=0.
过点P且与⊙C相切的直线方程:ax+by-r2=0.
将圆化为标准方程得:a2+b2=r2,
∴圆心(0,0),半径为:r,
∵(a,b)与(0,0)连线的斜率为
| b |
| a |
∴切线的斜率为-
| a |
| b |
则切线方程为y-b=-
| a |
| b |
过点P且与⊙C相切的直线方程:ax+by-r2=0.
点评:此题考查了圆的标准方程,以及圆的切线方程,当直线与圆相切时,圆心到切线的距离等于圆的半径,熟练掌握此性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=
,若f(m)>1,则m的取值范围是( )
|
| A、(-∞,-1) |
| B、(9,+∞) |
| C、(-∞,-1)∪(9,+∞) |
| D、(-∞,-1)∪(6,+∞) |
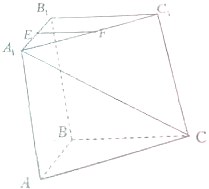 已知如图,在直三棱柱ABC-A1B1C1中(侧棱垂直底面内所有直线的棱柱叫做
已知如图,在直三棱柱ABC-A1B1C1中(侧棱垂直底面内所有直线的棱柱叫做