题目内容
已知一个袋中装有3个白球和3个红球,这些球除颜色外完全相同.
(1)每次从袋中取一个球,取出后不放回,直到取到一个红球为止,求取球次数ξ的分布列,数学期望E(ξ)和方差D(ξ).
(2)每次从袋中取一个球,取出后放回接着再取一个球,这样取3次,求取出红球次数η的数学期望.
(1)每次从袋中取一个球,取出后不放回,直到取到一个红球为止,求取球次数ξ的分布列,数学期望E(ξ)和方差D(ξ).
(2)每次从袋中取一个球,取出后放回接着再取一个球,这样取3次,求取出红球次数η的数学期望.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(1)取到1个红球为止,这是目标,那么取球次数ξ的最小值为1,最大值为4,求出对应值的概率,由此能求出取球次数ξ的分布列,数学期望E(ξ)和方差D(ξ).
(2)取出后放回,这是条件,所以每一次取到红球队的概率相同,这就相当于做了三次独立重复试验.由此得到取出红球次数η~B(3,
),从而能求出E(η).
(2)取出后放回,这是条件,所以每一次取到红球队的概率相同,这就相当于做了三次独立重复试验.由此得到取出红球次数η~B(3,
| 1 |
| 2 |
解答:
解:(1)由题意知ξ的可能取值为1,2,3,4,
P(ξ=1)=
=
,
P(ξ=2)=
=
=
,
P(ξ=3)=
=
=
,
P(ξ=4)=
=
=
,
∴ξ的分布列为:
E(ξ)=1×
+2×
+3×
+4×
=
,
D(ξ)=(1-
)2•
+(2-
)2×
+(3-
)2×
+(4-
)2×
=
.
(2)取出后放回,取球3次相当于3次独立重复试验,
∴取出红球次数η~B(3,
),
∴E(η)=3×
=
.
P(ξ=1)=
| 3 |
| 6 |
| 1 |
| 2 |
P(ξ=2)=
| ||||
|
| 3×3 |
| 6×5 |
| 3 |
| 10 |
P(ξ=3)=
| ||||
|
| 3×2×3 |
| 6×5×4 |
| 3 |
| 20 |
P(ξ=4)=
| ||||
|
| 3×2×3 |
| 6×5×4×3 |
| 1 |
| 20 |
∴ξ的分布列为:
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 1 |
| 2 |
| 3 |
| 10 |
| 3 |
| 20 |
| 1 |
| 20 |
| 7 |
| 4 |
D(ξ)=(1-
| 7 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
| 3 |
| 10 |
| 7 |
| 4 |
| 3 |
| 20 |
| 7 |
| 4 |
| 1 |
| 20 |
| 63 |
| 80 |
(2)取出后放回,取球3次相当于3次独立重复试验,
∴取出红球次数η~B(3,
| 1 |
| 2 |
∴E(η)=3×
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查离散型随机变量的分布列、数学期望、方差的求法,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
相关题目
| 3 |
| i |
| A、-3i | ||
B、-
| ||
| C、i | ||
| D、-i |
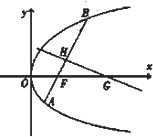 已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.
已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.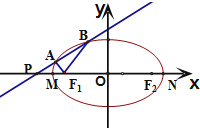 已知椭圆E:
已知椭圆E: