题目内容
定义在R上的奇函数f(x)满足:x<0时,f(x)=(
)x,则f(1)= .
| 1 |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:依题意,f(x)为R上的奇函数,从而可求得f(1)=-f(-1)的值.
解答:
解:由x<0时,f(x)=(
)x,
∴f(-1)=(
)-1=2,
f(x)为R上的奇函数得f(1)=-f(-1)=-2,
故答案为:-2.
| 1 |
| 2 |
∴f(-1)=(
| 1 |
| 2 |
f(x)为R上的奇函数得f(1)=-f(-1)=-2,
故答案为:-2.
点评:本题考查函数的求值,着重考查函数奇偶性的性质及应用,求得b的值是关键,属于基础题.

练习册系列答案
相关题目
在△ABC中,
2+
•
<0,则△ABC为( )
| AB |
| AB |
| BC |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角或钝角三角形 |
在△ABC中,若三个内角A,B,C成等差数列且A<B<C,则cosAcosC的取值范围是( )
A、(-
| ||||
B、[-
| ||||
C、(-
| ||||
D、(-
|
已知函数f(x)=sin2x+2
cos2x-
,函数g(x)=mcos(2x-
)-2m+3(m>0),若?x1∈[0,
],总?x2∈[0,
],使得g(x1)=f(x2)成立,则实数m的取值范围为( )
| 3 |
| 3 |
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
| A、[1,2] | ||||
B、[1,
| ||||
C、[
| ||||
D、[
|
不等式组
表示的平面区域面积是( )
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
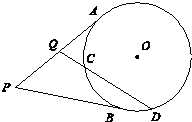 如图,p为⊙O外一点,过P点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=4,则PB=
如图,p为⊙O外一点,过P点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=4,则PB=