题目内容
17.我国古代有着辉煌的数学研究成果.《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、…、《辑古算经》等算经十书,有着十分丰富多彩的内容,是了解我国古代数学的重要文献.这10部专著中有7部产生于魏晋南北朝时期.某中学拟从这10部名著中选择2部作为“数学文化”校本课程学习内容,则所选2部名著中至少有一部是魏晋南北朝时期的名著的概率为$\frac{14}{15}$.分析 先求出从10部名著中选择2部名著的方法数,再分别求出2部都为魏晋南北朝时期的名著的方法数和只有1部为魏晋南北朝时期的名著的方法数,由此利用互斥事件概率加法公式能求出事件“所选两部名著中至少有一部是魏晋南北朝时期的名著”的概率.
解答 解:从10部名著中选择2部名著的方法数为9+8+7+6+5+4+3+2+1=45种,
2部都为魏晋南北朝时期的名著的方法数为6+5+4+3+2+1=21种,
只有1部为魏晋南北朝时期的名著的方法数为7×3=21种,
∴事件“所选两部名著中至少有一部是魏晋南北朝时期的名著”的概率:p=$\frac{42}{45}$=$\frac{14}{15}$.
故答案为:$\frac{14}{15}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意互斥事件概率加法公式的合理运用.

练习册系列答案
相关题目
5.已知i为虚数单位,则复数$\frac{(1-i)^{3}}{(1+i)^{2}}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.与椭圆$C:\frac{x^2}{9}+\frac{y^2}{5}=1$共焦点且过点$P(3,\sqrt{2})$的双曲线方程为( )
| A. | ${x^2}-\frac{y^2}{3}=1$ | B. | $\frac{x^2}{3}-{y^2}=1$ | C. | $\frac{x^2}{2}-\frac{y^2}{6}=1$ | D. | $\frac{x^2}{6}-\frac{y^2}{2}=1$ |
6.已知m,n∈R,则“mn<0”是“抛物线mx2+ny=0的焦点在y轴正半轴上”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
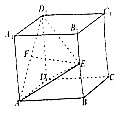 如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.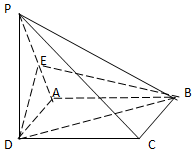 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证:
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证: