题目内容
7.从分别写有1,2,3,4,5的五张卡片中依次抽取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则取到的两张卡片上的数字之和为偶数的概率为$\frac{2}{5}$.分析 先基本事件总数n=${C}_{5}^{2}$=10,再求出取到的两张卡片上的数字之和为偶数包含的基本事件个数:m=${C}_{3}^{2}+{C}_{2}^{2}$=4,由此能求出取到的两张卡片上的数字之和为偶数的概率.
解答 解:从分别写有1,2,3,4,5的五张卡片中依次抽取两张,
假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,
基本事件总数n=${C}_{5}^{2}$=10,
取到的两张卡片上的数字之和为偶数包含的基本事件个数:
m=${C}_{3}^{2}+{C}_{2}^{2}$=4,
∴取到的两张卡片上的数字之和为偶数的概率为p=$\frac{4}{10}$=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
18.在△ABC中,已知a:b:c=3:2:4,那么cosC=( )
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{1}{4}$ |
2.下列命题是真命题的为( )
| A. | ?x∈R,2x>1 | B. | ?x∈R,x2>0 | C. | ?x∈R,2x<1 | D. | ?x∈R,x2<0 |
12.两直线3x+y-3=0与3x+my+$\frac{1}{2}$=0平行,则它们之间的距离是( )
| A. | 4 | B. | $\frac{2}{13}$$\sqrt{13}$ | C. | $\frac{5}{26}$$\sqrt{13}$ | D. | $\frac{7}{20}$$\sqrt{10}$ |
19.若关于x的一元二次方程x2+ax-2=0有两个不相等的实根x1,x2,且x1<-1,x2>1,则实数a的取值范围是( )
| A. | a<-1 | B. | a>1 | C. | -1<a<1 | D. | a>2$\sqrt{2}$或a<-2$\sqrt{2}$ |
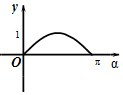
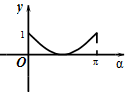
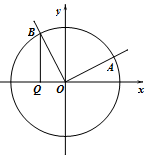 如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )
如图,在平面直角坐标系xOy中,角α(0≤α≤π)的始边为x轴的非负半轴,终边与单位圆的交点为A,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB,过点B作x轴的垂线,垂足为Q.记线段BQ的长为y,则函数y=f(α)的图象大致是( )