题目内容
12.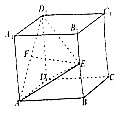 如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=AA1=2,∠ABC=120°,E,F分别为BB1、AD1的中点.(1)求证;平面D1AE⊥平面ADD1A1;
(2)求三棱锥D-D1AE的体积.
分析 (1)取AD的中点M,连接FM.BM,则BMFE是平行四边形,证明BM⊥平面ADD1A1,可得EF⊥平面ADD1A1,即可证明结论;
(2)利用等体积转化,求三棱锥D-D1AE的体积.
解答 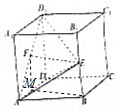 (1)证明:取AD的中点M,连接FM.BM,则BMFE是平行四边形,
(1)证明:取AD的中点M,连接FM.BM,则BMFE是平行四边形,
∴BM∥EF,
∵四边形ABCD是菱形,∠ABC=120°,
∴BM⊥AD,
∵直四棱柱ABCD-A1B1C1D1,
∴BM⊥平面ADD1A1,
∴EF⊥平面ADD1A1,
∵EF?平面D1AE
∴平面D1AE⊥平面ADD1A1;
(2)解:由(1)知,EF=BM=$\sqrt{3}$,
∴三棱锥D-D1AE的体积V=$\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{3}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查线面垂直,面面垂直的证明,考查三棱锥体积的计算,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
2.已知函数f(x)=a-x2(1≤x≤2)与g(x)=2x+1的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | [-2,-1] | B. | [-1,1] | C. | [1,3] | D. | [3,+∞] |
2.下列命题是真命题的为( )
| A. | ?x∈R,2x>1 | B. | ?x∈R,x2>0 | C. | ?x∈R,2x<1 | D. | ?x∈R,x2<0 |