题目内容
已知抛物线y=x2+bx+c在点(1,2)处的切线与直线x+y+2=0垂直,求函数y=x2+bx+c的最值.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出函数的导数,根据导数的几何意义,求出b,c的值,利用二次函数的性质即可得到结论.
解答:
解:∵y=x2+bx+c,
∴函数的导数为f′(x)=2x+b,
∴抛物线在点(1,2)处的切线斜率k=2+b,
∵切线与直线x+y+2=0垂直,
∴2+b=1,即b=-1,
∵点(1,2)也在抛物线上,
∴1+b+c=2,得c=2.
即函数y=x2+bx+c=x2-x+2=(x-
)2+
,
∴当x=
时,函数取得最小值
,函数无最大值.
∴函数的导数为f′(x)=2x+b,
∴抛物线在点(1,2)处的切线斜率k=2+b,
∵切线与直线x+y+2=0垂直,
∴2+b=1,即b=-1,
∵点(1,2)也在抛物线上,
∴1+b+c=2,得c=2.
即函数y=x2+bx+c=x2-x+2=(x-
| 1 |
| 2 |
| 7 |
| 4 |
∴当x=
| 1 |
| 2 |
| 7 |
| 4 |
点评:本题主要考查导数的几何意义,以及直线垂直的性质,要求熟练掌握导数的几何意义.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
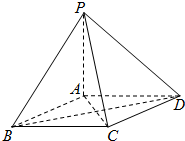 如图,四棱锥P-ABCD的俯视图是菱形ABCD,顶点P的投影恰好为A.
如图,四棱锥P-ABCD的俯视图是菱形ABCD,顶点P的投影恰好为A.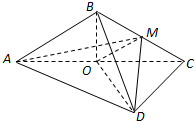 菱形ABCD的边长为3,AC与BD交于O,且∠BAD=60°.将菱形ABCD沿对角线AC折起得到三棱锥B-ADC(如图),点M是棱BC的中点,DM=
菱形ABCD的边长为3,AC与BD交于O,且∠BAD=60°.将菱形ABCD沿对角线AC折起得到三棱锥B-ADC(如图),点M是棱BC的中点,DM=