题目内容
已知函数f(x)=ax2-4x+2,
(1)若f(2-x)=f(2+x),求f(x)的解析式;
(2)已知a≤1,若函数y=f(x)-log2
在区间[1,2]内有且只有一个零点,试确定实数a的取值范围.
(1)若f(2-x)=f(2+x),求f(x)的解析式;
(2)已知a≤1,若函数y=f(x)-log2
| x |
| 8 |
考点:函数解析式的求解及常用方法,函数零点的判定定理
专题:函数的性质及应用
分析:(1)先求出函数的对称轴,从而求出a的值,进而求出函数f(x)的表达式;
(2)设r(x)=ax2-4x+5,s(x)=log2x(x∈[1,2]),问题转化为两个函数r(x)与s(x)的图象在区间[1,2]内有唯一交点,通过讨论a的范围,结合函数的单调性,从而求出a的范围.
(2)设r(x)=ax2-4x+5,s(x)=log2x(x∈[1,2]),问题转化为两个函数r(x)与s(x)的图象在区间[1,2]内有唯一交点,通过讨论a的范围,结合函数的单调性,从而求出a的范围.
解答:
解:(1)∵f(2-x)=f(2+x),
∴f(x)的对称轴为x=2,
即-
=2,即a=1,
∴f(x)=x2-4x+2.
(2)因为y=f(x)-log2
=ax2-4x+5-log2x
设r(x)=ax2-4x+5,s(x)=log2x(x∈[1,2])
则原命题等价于两个函数r(x)与s(x)的图象在区间[1,2]内有唯一交点
当a=0时,r(x)=-4x+5在区间[1,2]内为减函数,s(x)=log2x(x∈[1,2])为增函数,
且r(1)=1>s(1)=0,r(2)=-3<s(2)=1,
所以函数r(x)与s(x)的图象在区间[1,2]内有唯一交点
当a<0时,r(x)图象开口向下,对称轴为x=
<0
所以r(x)在区间[1,2]内为减函数,s(x)=log2x(x∈[1,2])为增函数,
则由
⇒
⇒-1≤a≤1,所以-1≤a<0,
当0<a≤1时,r(x)图象开口向上,对称轴为x=
≥2,
所以r(x)在区间[1,2]内为减函数,s(x)=log2x(x∈[1,2])为增函数,
则由
⇒
⇒-1≤a≤1,所以0<a≤1,
综上所述,实数a的取值范围为[-1,1].
∴f(x)的对称轴为x=2,
即-
| 4 |
| 2a |
∴f(x)=x2-4x+2.
(2)因为y=f(x)-log2
| x |
| 8 |
设r(x)=ax2-4x+5,s(x)=log2x(x∈[1,2])
则原命题等价于两个函数r(x)与s(x)的图象在区间[1,2]内有唯一交点
当a=0时,r(x)=-4x+5在区间[1,2]内为减函数,s(x)=log2x(x∈[1,2])为增函数,
且r(1)=1>s(1)=0,r(2)=-3<s(2)=1,
所以函数r(x)与s(x)的图象在区间[1,2]内有唯一交点
当a<0时,r(x)图象开口向下,对称轴为x=
| 2 |
| a |
所以r(x)在区间[1,2]内为减函数,s(x)=log2x(x∈[1,2])为增函数,
则由
|
|
当0<a≤1时,r(x)图象开口向上,对称轴为x=
| 2 |
| a |
所以r(x)在区间[1,2]内为减函数,s(x)=log2x(x∈[1,2])为增函数,
则由
|
|
综上所述,实数a的取值范围为[-1,1].
点评:本题考查了求函数的解析式问题,考查了函数的单调性,考查了分类讨论思想,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
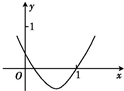 如图是二次函数f(x)=
如图是二次函数f(x)=| 1 |
| 2 |
A、(
| ||||
B、(
| ||||
| C、(1,2) | ||||
| D、(2,3) |
△ABC中,角A,B,C所对边的长分别为a,b,c,若a2+b2=2c2,则cosC的最小值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
已知实数a,b,则a•b>0是a>0且b>0的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |