题目内容
14．已知点P在圆x2+y2-2x+4y+1=0上，点Q在不等式$\left\{\begin{array}{l}{x+y≥2}\\{0≤y≤1}\end{array}\right.$，表示的平面区域内，则线段PQ长的最小值是$\sqrt{5}-2$．分析 化圆的方程为标准方程，求出圆心坐标和半径，画出图形，数形结合得答案．
解答 解：化x2+y2-2x+4y+1=0为（x-1）2+（y+2）2=4，
由题意画出图形如图，
由图可知，|CQ|=$\sqrt{（2-1）^{2}+{2}^{2}}=\sqrt{5}$，
∴线段PQ长的最小值是$\sqrt{5}-2$．
故答案为：$\sqrt{5}-2$．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
9．
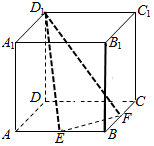如图，正方体ABCD-A1B1C1D1中，E、F分别是AB、BC的中点，过点D1、E、F的截面将正方体分割成两个部分，记这两个部分的体积分别为V1、V2（V1＜V2），则V1：V2=（ ）
如图，正方体ABCD-A1B1C1D1中，E、F分别是AB、BC的中点，过点D1、E、F的截面将正方体分割成两个部分，记这两个部分的体积分别为V1、V2（V1＜V2），则V1：V2=（ ）| A． | $\frac{1}{3}$ | B． | $\frac{3}{5}$ | C． | $\frac{25}{47}$ | D． | $\frac{7}{9}$ |
19．将函数f（x）=xsinx，当${x_1}，{x_2}∈[-\frac{π}{2}，\frac{π}{2}]$时，f（x1）＞f（x2）成立，下列结论正确的是（ ）
| A． | x1＞x2 | B． | x1＞|x2| | C． | x1＜x2 | D． | x${\;}_{1}^{2}$＞x${\;}_{2}^{2}$ |
6．已知i是虚数单位，若$z（{1-\frac{1}{2}i}）=\frac{1}{2}i$，则|Z|=（ ）
| A． | 1 | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\sqrt{5}$ | D． | $\frac{{\sqrt{5}}}{5}$ |
4．$tanϕ=-\sqrt{3}$，ϕ为第四象限角，则cosϕ=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | -$\frac{{\sqrt{3}}}{2}$ |