题目内容
2.已知函数f(x)=x3-3x2-9x+11(Ⅰ)求函数f(x)的递减区间.
(Ⅱ)讨论函数f(x)的极值情况,如有,求出极值.
分析 求出函数的导数,解关于导函数的不等式,列出表格;(Ⅰ)根据表格求出函数的递减区间即可;(Ⅱ)根据表格求出函数的极值即可.
解答 解:f′(x)=3x2-6x-9=3(x+1)(x-3),…(3分)
令f′(x)=0,得x1=-1,x2=3.…(5分)
x变化时,f′(x)的符号变化情况及f(x)的增减性如下表所示:
| x | (-∞,-1) | -1 | (-1,3) | 3 | (3,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 f(-1) | 减 | 极小值 f(3) | 增 |
(Ⅱ)由表可得,当x=-1时,函数有极大值为f(-1)=16;
当x=3时,函数有极小值为f(3)=-16.…(13分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
14. 如图,函数y=log24x图象上的两点A,B和y=log2x上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则p2×2q=( )
如图,函数y=log24x图象上的两点A,B和y=log2x上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则p2×2q=( )
 如图,函数y=log24x图象上的两点A,B和y=log2x上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则p2×2q=( )
如图,函数y=log24x图象上的两点A,B和y=log2x上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则p2×2q=( )| A. | 12 | B. | $12\sqrt{3}$ | C. | 6 | D. | $6\sqrt{3}$ |
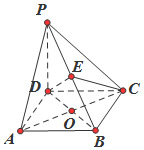 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2$\sqrt{3}$,且AC,BD交于点O,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2$\sqrt{3}$,且AC,BD交于点O,E是PB上任意一点. 如图所示,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB=2
如图所示,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB=2 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(12,5)=2,下面是一个算法的程序框图,当输入的n为77时,则输出的结果为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(12,5)=2,下面是一个算法的程序框图,当输入的n为77时,则输出的结果为( )