题目内容
已知xy=4 （x＞0，y＞0），x+y的最小值是M，则M= ．
考点：基本不等式在最值问题中的应用
专题：不等式的解法及应用
分析：根据不等式x+y≥2
求解即可．
| xy |
解答：
解：∵xy=4 （x＞0，y＞0），
x+y≥2
=2
=4，（x=y=2时等号成立）
∴x+y的最小值是4，
故答案为：4
x+y≥2
| xy |
| 4 |
∴x+y的最小值是4，
故答案为：4
点评：本题考查了基本不等式的运用，属于容易题．
练习册系列答案
相关题目
设a=sin（cos2015°），b=sin（sin2015°），c=cos（sin2015°），d=cos（cos2015°），则（ ）
| A、d＞c＞b＞a |
| B、d＞c＞a＞b |
| C、c＞d＞a＞b |
| D、c＞d＞b＞a |
将函数f(x)=sin(2x+
)的图象向左平移n（n＞0）个单位，再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为偶函数，则n的最小值为（ ）
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=sinx-tanx的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |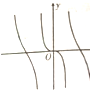
下列函数中，不满足f（2x）=2f（x）的是（ ）
| A、f（x）=x+1 |
| B、f（x）=x-|x| |
| C、f（x）=|x| |
| D、f（x）=-x |