题目内容
4.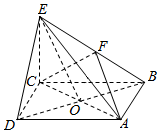 如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.(1)求证:DE∥平面ACF;
(2)若AB=$\sqrt{2}$CE,在线段EO上是否存在点G,使得CG⊥平面BDE?若存在,请证明你的结论;若不存在,请说明理由.
分析 (1)利用正方形的性质以及中线性质任意得到OF∥DE,利用线面平行的判定定理可证;
(2)取EO的中点G,连接CG,可证CG⊥EO,由EC⊥BD,AC⊥BD,可得平面ACE⊥平面BDE,从而利用面面垂直的性质即可证明CG⊥平面BDE.
解答 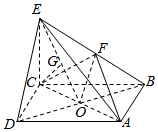 (本题满分为14分)证明:(1)连接OF由四边形ABCD是正方形可知,点O为BD的中点,又F为BE的中点,
(本题满分为14分)证明:(1)连接OF由四边形ABCD是正方形可知,点O为BD的中点,又F为BE的中点,
所以OF∥DE.…(2分)
又OF?平面ACF,DE?平面ACF,
所以DE∥平面ACF.…(6分)
(2)在线段EO上存在点G,使CG⊥平面BDE,
证明如下:取EO的中点G,连接CG,在四棱锥E-ABCD中,AB=$\sqrt{2}$CE,CO=$\frac{\sqrt{2}}{2}$AB=CE,
所以CG⊥EO.…(8分)
又由EC⊥底面ABCD,BD?底面ABCD,
所以EC⊥BD.…(10分)
由四边形ABCD是正方形可知,AC⊥BD,又AC∩EC=C,
所以BD⊥平面ACE,而BD?平面BDE,…(12分)
所以,平面ACE⊥平面BDE,且平面ACE∩平面BDE=EO,
因为CG⊥EO,CG?平面ACE,
所以CG⊥平面BDE.…(14分)
点评 本题主要考查了线面平行的判定定理以及线面垂直的判定定理和性质定理的运用,考查了空间想象能力和推理论证能力,关键是熟练掌握相关定理的条件及结论,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
14.已知函数f(x)在定义域[2-a,3]上是偶函数,在[0,3]上单调递增,并且f(-m2-$\frac{a}{5}$)>f(-m2+2m-2),则m的取值范围是( )
| A. | $(1-\sqrt{2},\sqrt{2}]$ | B. | $[1-\sqrt{2},\sqrt{2}]$ | C. | $[\frac{1}{2},\sqrt{2}]$ | D. | $(\frac{1}{2},\sqrt{2}]$ |
12.等比数列{an}中,a2=9,a5=243,则a1与a7的等比中项为( )
| A. | ±81 | B. | 81 | C. | -81 | D. | 27 |
16.已知随机变量X~B(6,$\frac{\sqrt{2}}{2}$),则P(X≤5)=( )
| A. | $\frac{7}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{63}{64}$ | D. | $\frac{31}{32}$ |