题目内容
14.已知函数f(x)在定义域[2-a,3]上是偶函数,在[0,3]上单调递增,并且f(-m2-$\frac{a}{5}$)>f(-m2+2m-2),则m的取值范围是( )| A. | $(1-\sqrt{2},\sqrt{2}]$ | B. | $[1-\sqrt{2},\sqrt{2}]$ | C. | $[\frac{1}{2},\sqrt{2}]$ | D. | $(\frac{1}{2},\sqrt{2}]$ |
分析 根据函数奇偶性的定义先求出a的值,根据函数奇偶性和单调性的性质将不等式进行转化进行求解即可.
解答 解:因为函数f(x)在定义域[2-a,3]上是偶函数,所以2-a+3=0,所以a=5.
所以$f(-{m^2}-\frac{a}{5})>f(-{m^2}+2m-2)$,即f(-m2-1)>f(-m2+2m-2),
所以函数f(x)在[-3,0]上单调递减,而-m2-1<0,-m2+2m-2=-(m-1)2-1<0,
所以由f(-m2-1)>f(-m2+2m-2)得,
$\left\{{\begin{array}{l}{-3≤-{m^2}-1≤0}\\{-3≤-{m^2}+2m-2≤0}\\{-{m^2}-1<-{m^2}+2m-2}\end{array}}\right.$,
解得$\frac{1}{2}<m≤\sqrt{2}$.
故选:D
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系,将不等式进行转化是解决本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
4.已知数列{an}的前n和为Sn,a1=1.当n≥2时,an+2Sn-1=n,则S2016=( )
| A. | $\frac{2015}{2}$ | B. | 1006 | C. | 1007 | D. | 1008 |
5.不等式(x2-x+1)(x-4)(6-x)>0的解集是( )
| A. | {x|x<4或x>6} | B. | {x|x<-6或x>-4} | C. | {x|4<x<6} | D. | 以上都不对 |
3.将函数y=sinx-$\sqrt{3}$cosx的图象沿x轴向右平移a个单位(a>0),所得图象关于y轴对称,则a的值可以是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{2}$ | C. | -$\frac{π}{6}$ | D. | $\frac{π}{3}$ |
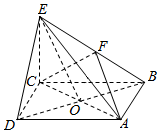 如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
如图,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.