题目内容
12．等比数列{an}中，a2=9，a5=243，则a1与a7的等比中项为（ ）| A． | ±81 | B． | 81 | C． | -81 | D． | 27 |
分析 利用等比数列的通项公式可得q．再利用等比中项的定义及其性质即可得出．
解答 解：设等比数列{an}的公比q，
∵a2=9，a5=243，
∴243=9×q3，解得q=3．
又a1•a7=${a}_{4}^{2}$，
∴a1与a7的等比中项为±a4=±${a}_{2}{q}^{2}$=±9×32=±81．
故选：A．
点评 本题考查了等比数列的通项公式及其性质、等比中项，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
3．将函数y=sinx-$\sqrt{3}$cosx的图象沿x轴向右平移a个单位（a＞0），所得图象关于y轴对称，则a的值可以是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{2}$ | C． | -$\frac{π}{6}$ | D． | $\frac{π}{3}$ |
7．在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，若△ABC的面积S=$\frac{1}{4}$（b2+c2-a2），∠A 的弧度数为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
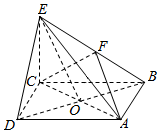如图，在四棱锥E-ABCD中，底面ABCD是正方形，AC与BD交于点O，EC⊥底面ABCD，F为BE的中点．